lunes, 29 de septiembre de 2008
viernes, 26 de septiembre de 2008
SUCESOS MUTUAMENTE EXCLUYENTES:
Exclulir significa "dejar fuera", de manera que dos sucesos seràn excluyentes si ellos no tienen elementos comunes (es decir uno excluye al otro).
COMENTARIO:
Es decir, que la intersección de ambos eventos es vacía. Si dos o más eventos no pueden ocurrir simultáneamente.
COMENTARIO:
Es decir, que la intersección de ambos eventos es vacía. Si dos o más eventos no pueden ocurrir simultáneamente.
AXIOMAS:
Un axioma es el elemento bàsico de un sistema de lògica formal y junto con las reglas de inferencia definen un sistema deductivo.
La palabra axioma proviene del griego αξιωμα (axioma), que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba.
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada.Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.
La probabilidad P de un suceso E, denotada por P(E), se define con respecto a un "universo" o espacio muestral Ω, conjunto de todos los posibles sucesos elementales, tal que P verifique los Axiomas de Kolmogórov, enunciados por el matemático ruso de este nombre en 1933. En este sentido, el suceso E es, en términos matemáticos, un subconjunto de Ω.
COMENTARIO:
Es una gramàtica formal capaz de representar cierto aspecto de la realidad.sin necesidad de demostraciòn es aquella que se considera verdadera sin ninguna necesidad de prueba. Es una forma de expresar lògicamente para llegar a una conclusiòn, que se clasifica en dos aspectos importantes las cuales se menciona; Axiomas lògicos: que son verdaderos en cualquier universo posible. Y se darà a conocer su fòrmula respectiva.
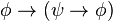


Los Axiomas no-lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo naturales, los axiomas no-lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no-lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no-lógicos es postulado.
Los axiomas no-lógicos esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aún sin la introducción de este axioma se puede desarrollar la terìa de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
La palabra axioma proviene del griego αξιωμα (axioma), que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba.
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada.Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.
La probabilidad P de un suceso E, denotada por P(E), se define con respecto a un "universo" o espacio muestral Ω, conjunto de todos los posibles sucesos elementales, tal que P verifique los Axiomas de Kolmogórov, enunciados por el matemático ruso de este nombre en 1933. En este sentido, el suceso E es, en términos matemáticos, un subconjunto de Ω.
COMENTARIO:
Es una gramàtica formal capaz de representar cierto aspecto de la realidad.sin necesidad de demostraciòn es aquella que se considera verdadera sin ninguna necesidad de prueba. Es una forma de expresar lògicamente para llegar a una conclusiòn, que se clasifica en dos aspectos importantes las cuales se menciona; Axiomas lògicos: que son verdaderos en cualquier universo posible. Y se darà a conocer su fòrmula respectiva.
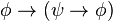


Los Axiomas no-lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo naturales, los axiomas no-lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no-lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no-lógicos es postulado.
Los axiomas no-lógicos esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aún sin la introducción de este axioma se puede desarrollar la terìa de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
ESPERANZA MATEMÀTICA:
Una definición fácil de entender de lo que aquí llamaremos «Esperanza Matemática» es la relación entre el premio obtenido y probabilidad de acertar.
La definición matemática de «Esperanza Matemática» o Valor Esperado es bastante más compleja, pero en el desarrollo de este Sistema se limita a Premio x Probabilidad. Aquí, un valor para la esperanza matemática de 1 indica «juego justo», un «menor que uno» indica «desfavorable para el jugador» y un «mayor que uno» es «favorable para el jugador» ( en las definiciones formales el cero suele ser el «juego justo», y los valores negativos o positivos indican «positivo o negativo para el jugador»).
Si la esperanza matemática es 1, el juego es «justo». Por ejemplo, apostar 1 euro a que una moneda sale cara o cruz, si el premio por acertar son 2 euros, y si se pierde, 0 euros. La esperanza del juego es 2 · (1/2) = 1. Entonces, consecuentemente con la teoría de juegos, podría pagar el euro para jugar o para rechazar jugar, porque de cualquier manera su expectativa total sería 0.
Si la esperanza matemática es menor que 1, el juego es «desfavorable para el jugador». Un sorteo que pague 500 a 1 pero en el que la probabilidad de acertar sea de 1 entre 1.000, la esperanza matemática es 500 · (1/1.000) = 0,5.
Si la esperanza matemática es mayor que 1, el juego es «favorable para el jugador», todo un «chollo» para el jugador. Un ejemplo sería un juego en el que se paga 10 a 1 por acertar el número que va a salir en un dado, en donde hay una probabilidad de acertar es de 1 entre 6. En este ejemplo el valor de la esperanza matemática es 10 · (1/6)=1,67 y por tanto en esas condiciones es juego «beneficioso» para el jugador.
Esperanza matemática de las loterías
La esperanza matemática es un valor importante que conocer para cualquier tipo de premio, en función de su dificultad, y para cada sorteo concreto.
En la Primitiva, la esperanza matemática general o promedio es sencillamente 0,55 y en Euromillones es 0,5. Se corresponde a la cantidad que se devuelve en premios: el 55% o el 50% del total apostado por los jugadores. Ese dinero siempre se devuelve, teniendo en cuenta que con el tiempo los premios no entregados se acumulan en Botes.
En la Primitiva el reparto de premios funciona de modo que la cantidad jugada por todos los jugadores (excepto el 45% que se queda la organización) se suma y reparte en diversas categorías: una parte para los de más aciertos, otra parte para premios menores, reintegros, etc. Esto marca ciertamente diferencias entre la esperanza matemática (premios por probabilidad) de las diferentes categorías de premios. La esperanza matemática más alta es la del Reintegro que es de 0,1 (10 %).
Estos cálculos, que de por sí son sencillos, se ven complicados por algunas reglas relativamente recientes, como el «premio fijo para los acertantes de 3» o «los acertantes de 5 nunca pueden ganar más que los de 6», pero son en cualquier caso calculables con precisión.
En general, y para la Loto tradicional la norma a grandes rasgos es que la esperanza matemática es mayor que 1 cuando la cantidad de premios total (el bote más el 55% de la cantidad que todos los jugadores apuestan ese día) es mayor de lo que valen 13,9 millones de apuestas (dado que la probabilidad de acertar es de 1 entre 13,9 millones) y esto ocurre en muy muy muy raras ocasiones.
Pero imagenemos como hipótesis de trabajo que llega un día en el que se ha acumulado un bote de 20 millones de euros y en el que por alguna circunstancia nadie juega a la Loto excepto una persona. A 1 euro por apuesta, esto supondría pagar unos 14 millones de euros para jugar a todas las combinaciones y embolsarse todos los premios: el bote más lógicamente la recuperación del 55% de lo apostado y un 10% en reintegros (7,7 millones de euros, correspondiente al resto de premios menores de 5, 4, reintegros, etc.) Resultado: apostando 14 millones se recuperarían 27,7 millones de euros. Casi otros 14 millones de beneficio. ¡Buen negocio!
Un ejemplo real fue el sorteo de Bonoloto (Loto 6/49) del 18/11/1990. Un bote de 1.151 millones de pesetas se sumó a una recaudación de sólo 374 millones. A 25 pesetas por apuesta se hicieron en total unos 15 millones de apuestas. La probabilidad de acertar 6 era de 1 entre 14 millones, como siempre (y en total se repartía el 55% de la recaudación, como siempre). El premio de 1.200 millones que recibió un único acertante de 6 números tenía como base una esperanza matemática de 3,2 (frente a 1 que sería lo normal en un “juego justo” o 0,55 en un día convencional sin bote). Es decir, si el juego hubiera sido “justo” tanto para el jugador como para la banca, el premio debería haber sido de sólo unos 350 millones. Pero el ganador se llevó 1.200 millones porque había un bote acumulado de muchísimas semanas. La esperanza matemática promedio de ese día, contando todos los premios, era de 3,6. ¡Ese día ciertamente era mejor jugar a la Loto que no jugar!
Casi siempre, cualquier juego real de apuestas tiene esperanza menor que 1: lo más probable es perder dinero. El motivo por el que se juega es que en caso de ganar, los premios son de escándalo. Estamos dispuestos a perder una cantidad pequeña de dinero casi con seguridad a cambio de la posibilidad, por pequeña que sea, de hacernos ricos de la noche a la mañana.
COMENTARIO:
Es aquella que asume diferentes valores a consecuencia de los resultados de un experimento aleatorio que es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. al igual nos ayuda a describir la tendencia, dispersiòn, asimetrìa, y apuntamiento de sus valores tales puede ser el consepto fundamental en el estudio de las distribuciones de probabilidad. En la cual se menciona la desviaciòn estàndar, los cuartiles, la asimetrìa que abarca de una funciòn numèrica que define la probabilidad de un conjunto dado. Esto es el mas comùn promedio utilizado. ya que para obtener el valor esperado se opera multiplicando cada valor que asume la probabilidad, de ocurrencia de ese valor y luego lo sumamos los productos. Que es un promedio de los resultados que se esperan en el futuro.
La definición matemática de «Esperanza Matemática» o Valor Esperado es bastante más compleja, pero en el desarrollo de este Sistema se limita a Premio x Probabilidad. Aquí, un valor para la esperanza matemática de 1 indica «juego justo», un «menor que uno» indica «desfavorable para el jugador» y un «mayor que uno» es «favorable para el jugador» ( en las definiciones formales el cero suele ser el «juego justo», y los valores negativos o positivos indican «positivo o negativo para el jugador»).
Si la esperanza matemática es 1, el juego es «justo». Por ejemplo, apostar 1 euro a que una moneda sale cara o cruz, si el premio por acertar son 2 euros, y si se pierde, 0 euros. La esperanza del juego es 2 · (1/2) = 1. Entonces, consecuentemente con la teoría de juegos, podría pagar el euro para jugar o para rechazar jugar, porque de cualquier manera su expectativa total sería 0.
Si la esperanza matemática es menor que 1, el juego es «desfavorable para el jugador». Un sorteo que pague 500 a 1 pero en el que la probabilidad de acertar sea de 1 entre 1.000, la esperanza matemática es 500 · (1/1.000) = 0,5.
Si la esperanza matemática es mayor que 1, el juego es «favorable para el jugador», todo un «chollo» para el jugador. Un ejemplo sería un juego en el que se paga 10 a 1 por acertar el número que va a salir en un dado, en donde hay una probabilidad de acertar es de 1 entre 6. En este ejemplo el valor de la esperanza matemática es 10 · (1/6)=1,67 y por tanto en esas condiciones es juego «beneficioso» para el jugador.
Esperanza matemática de las loterías
La esperanza matemática es un valor importante que conocer para cualquier tipo de premio, en función de su dificultad, y para cada sorteo concreto.
En la Primitiva, la esperanza matemática general o promedio es sencillamente 0,55 y en Euromillones es 0,5. Se corresponde a la cantidad que se devuelve en premios: el 55% o el 50% del total apostado por los jugadores. Ese dinero siempre se devuelve, teniendo en cuenta que con el tiempo los premios no entregados se acumulan en Botes.
En la Primitiva el reparto de premios funciona de modo que la cantidad jugada por todos los jugadores (excepto el 45% que se queda la organización) se suma y reparte en diversas categorías: una parte para los de más aciertos, otra parte para premios menores, reintegros, etc. Esto marca ciertamente diferencias entre la esperanza matemática (premios por probabilidad) de las diferentes categorías de premios. La esperanza matemática más alta es la del Reintegro que es de 0,1 (10 %).
Estos cálculos, que de por sí son sencillos, se ven complicados por algunas reglas relativamente recientes, como el «premio fijo para los acertantes de 3» o «los acertantes de 5 nunca pueden ganar más que los de 6», pero son en cualquier caso calculables con precisión.
En general, y para la Loto tradicional la norma a grandes rasgos es que la esperanza matemática es mayor que 1 cuando la cantidad de premios total (el bote más el 55% de la cantidad que todos los jugadores apuestan ese día) es mayor de lo que valen 13,9 millones de apuestas (dado que la probabilidad de acertar es de 1 entre 13,9 millones) y esto ocurre en muy muy muy raras ocasiones.
Pero imagenemos como hipótesis de trabajo que llega un día en el que se ha acumulado un bote de 20 millones de euros y en el que por alguna circunstancia nadie juega a la Loto excepto una persona. A 1 euro por apuesta, esto supondría pagar unos 14 millones de euros para jugar a todas las combinaciones y embolsarse todos los premios: el bote más lógicamente la recuperación del 55% de lo apostado y un 10% en reintegros (7,7 millones de euros, correspondiente al resto de premios menores de 5, 4, reintegros, etc.) Resultado: apostando 14 millones se recuperarían 27,7 millones de euros. Casi otros 14 millones de beneficio. ¡Buen negocio!
Un ejemplo real fue el sorteo de Bonoloto (Loto 6/49) del 18/11/1990. Un bote de 1.151 millones de pesetas se sumó a una recaudación de sólo 374 millones. A 25 pesetas por apuesta se hicieron en total unos 15 millones de apuestas. La probabilidad de acertar 6 era de 1 entre 14 millones, como siempre (y en total se repartía el 55% de la recaudación, como siempre). El premio de 1.200 millones que recibió un único acertante de 6 números tenía como base una esperanza matemática de 3,2 (frente a 1 que sería lo normal en un “juego justo” o 0,55 en un día convencional sin bote). Es decir, si el juego hubiera sido “justo” tanto para el jugador como para la banca, el premio debería haber sido de sólo unos 350 millones. Pero el ganador se llevó 1.200 millones porque había un bote acumulado de muchísimas semanas. La esperanza matemática promedio de ese día, contando todos los premios, era de 3,6. ¡Ese día ciertamente era mejor jugar a la Loto que no jugar!
Casi siempre, cualquier juego real de apuestas tiene esperanza menor que 1: lo más probable es perder dinero. El motivo por el que se juega es que en caso de ganar, los premios son de escándalo. Estamos dispuestos a perder una cantidad pequeña de dinero casi con seguridad a cambio de la posibilidad, por pequeña que sea, de hacernos ricos de la noche a la mañana.
COMENTARIO:
Es aquella que asume diferentes valores a consecuencia de los resultados de un experimento aleatorio que es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. al igual nos ayuda a describir la tendencia, dispersiòn, asimetrìa, y apuntamiento de sus valores tales puede ser el consepto fundamental en el estudio de las distribuciones de probabilidad. En la cual se menciona la desviaciòn estàndar, los cuartiles, la asimetrìa que abarca de una funciòn numèrica que define la probabilidad de un conjunto dado. Esto es el mas comùn promedio utilizado. ya que para obtener el valor esperado se opera multiplicando cada valor que asume la probabilidad, de ocurrencia de ese valor y luego lo sumamos los productos. Que es un promedio de los resultados que se esperan en el futuro.
jueves, 25 de septiembre de 2008
RESULTADO:
Resultado. Es una consecuencia particular de un experimento.
COMENTARIO: esto nos señala de que debemos de encontrar la lògica de lo que queremos obtener de un eventos experimentado. o ya sea obteniendo datos exactos de una operacion de eventos ocurrentes.
COMENTARIO: esto nos señala de que debemos de encontrar la lògica de lo que queremos obtener de un eventos experimentado. o ya sea obteniendo datos exactos de una operacion de eventos ocurrentes.
EXPERIMENTOS:
Experimento. Es un proceso que lleva a la ocurrencia de una y sólo una de varias observaciones posibles.
COMENTARIO:
es cuando observamos un suceso y atravès de ellas encontramos posibles resultados por la cual queremos llegar a conocer.
COMENTARIO:
es cuando observamos un suceso y atravès de ellas encontramos posibles resultados por la cual queremos llegar a conocer.
LA PROBABILIDAD:
Probabilidad. Es un valor entre uno y cero, inclusive, que describe la posibilidad de que ocurra un resultado o evento determinado como consecuencia de la realización de un experimento
COMENTARIO:
Por medio de ella nos permite describir la posibilidad de que ocurra un resultado de dicho proceso que conlleva a la ocurrencia de una o varias observaciones posibles.
COMENTARIO:
Por medio de ella nos permite describir la posibilidad de que ocurra un resultado de dicho proceso que conlleva a la ocurrencia de una o varias observaciones posibles.
Reglas de Multiplicación
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
Los valores de los parámetros de la distribución de probabilidad normal son = 0 y = 1. Cualquier conjunto de valores X normalmente distribuido pueden convertirse en valores normales estándar z por medio de la formula:
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
Los valores de los parámetros de la distribución de probabilidad normal son = 0 y = 1. Cualquier conjunto de valores X normalmente distribuido pueden convertirse en valores normales estándar z por medio de la formula:
REGLAS DE MULTIPLICACION:
Reglas de Multiplicación
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
COMENTARIO:
esto nos indica que la ocurrencia de eventos se interceda entre los conjuntos posibles y que sean independientes o dependientes y como tambien representa una muestra en la cual es una campana. y atravès de ella marca motivos distintos y bàsicamente se obtiene aproximando distribuciones de probabilidad..
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
COMENTARIO:
esto nos indica que la ocurrencia de eventos se interceda entre los conjuntos posibles y que sean independientes o dependientes y como tambien representa una muestra en la cual es una campana. y atravès de ella marca motivos distintos y bàsicamente se obtiene aproximando distribuciones de probabilidad..
EVENTOS DEPENDIENTES:
Eventos dependientes
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(AB) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que AB no es una fracción.
P(AB) = P(A y B)/P(B) o P(BA) = P(A y B)/P(A)
COMENTARIO:
Consiste en hallar la probabilidad de que al extraer cualquiera de ellas ambas sea de otro gènero, ya sea marcando la diferencia entre ambas.
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(AB) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que AB no es una fracción.
P(AB) = P(A y B)/P(B) o P(BA) = P(A y B)/P(A)
COMENTARIO:
Consiste en hallar la probabilidad de que al extraer cualquiera de ellas ambas sea de otro gènero, ya sea marcando la diferencia entre ambas.
EVENTOS INDEPENDIENTES:
Eventos Independientes
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Ejemplo:
lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento.
COMENTARIO:
Son eventos que se ocurre y que no depende de otros ya que una vez tomada el objeto se regresa de nuevo a la probabilidad donde se obtuvo en el caso de la moneda como se menciona anteriormente.
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Ejemplo:
lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento.
COMENTARIO:
Son eventos que se ocurre y que no depende de otros ya que una vez tomada el objeto se regresa de nuevo a la probabilidad donde se obtuvo en el caso de la moneda como se menciona anteriormente.
EL ENFOQUE SUBJETIVO:
El enfoque subjetivo
Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal.
COMENTARIO :
CONSISTE EN EVENTOS QUE OCURRE EL INDIVIDUO DEPENDE DEL NIVEL DE CREENCIA QUE TIENE QUE BASA TAMBIEN EN LO QUE ES ADECUADO CUANDO HAY SOLO UNA OPORTUNIDAD DE REALIZARLO .
Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal.
COMENTARIO :
CONSISTE EN EVENTOS QUE OCURRE EL INDIVIDUO DEPENDE DEL NIVEL DE CREENCIA QUE TIENE QUE BASA TAMBIEN EN LO QUE ES ADECUADO CUANDO HAY SOLO UNA OPORTUNIDAD DE REALIZARLO .
EL ENFOQUE DE FRECUENCIA RELATIVA:
El enfoque de frecuencia relativa
También llamado Enfoque Empírico, determina la probabilidad sobre la base de la proporción de veces que ocurre un evento favorable en un numero de observaciones. En este enfoque no ese utiliza la suposición previa de aleatoriedad. Porque la determinación de los valores de probabilidad se basa en la observación y recopilación de datos.
Ejemplo:
Se ha observado que 9 de cada 50 vehículos que pasan por una esquina no tienen cinturón de seguridad. Si un vigilante de transito se para en esa misma esquina un ida cualquiera ¿Cuál será la probabilidad de que detenga un vehículo sin cinturón de seguridad?

COMENTARIO:
ESTOS NOS INDICA QUE TIENE LÌMITE LA OBSERVACION QUE QUEREMOS REALIZAR Y TAMBIEN IMPLICA OBTENER DATOS EXACTOS. Y SE DEBE SUPONER ALEATORIAMENTE UN ENFOQUE.
También llamado Enfoque Empírico, determina la probabilidad sobre la base de la proporción de veces que ocurre un evento favorable en un numero de observaciones. En este enfoque no ese utiliza la suposición previa de aleatoriedad. Porque la determinación de los valores de probabilidad se basa en la observación y recopilación de datos.
Ejemplo:
Se ha observado que 9 de cada 50 vehículos que pasan por una esquina no tienen cinturón de seguridad. Si un vigilante de transito se para en esa misma esquina un ida cualquiera ¿Cuál será la probabilidad de que detenga un vehículo sin cinturón de seguridad?
COMENTARIO:
ESTOS NOS INDICA QUE TIENE LÌMITE LA OBSERVACION QUE QUEREMOS REALIZAR Y TAMBIEN IMPLICA OBTENER DATOS EXACTOS. Y SE DEBE SUPONER ALEATORIAMENTE UN ENFOQUE.
EL ENFOQUE CLÀSICO:
El enfoque clásico
Dice que si hay x posibles resultados favorables a la ocurrencia de un evento A y z posibles resultados desfavorables a la ocurrencia de A, y todos los resultados son igualmente posibles y mutuamente excluyente (no pueden ocurrir los dos al mismo tiempo), entonces la probabilidad de que ocurra A es:
El enfoque clásico de la probabilidad se basa en la suposición de que cada resultado sea igualmente posible.
Este enfoque es llamado enfoque a priori porque permite, (en caso de que pueda aplicarse) calcular el valor de probabilidad antes de observar cualquier evento de muestra.
Ejemplo:
Si tenemos en una caja 15 piedras verdes y 9 piedras rojas. La probabilidad de sacar una piedra roja en un intento es:

COMENTARIO: estos nos indica que todos los eventos propramados o planteados tiene la misma probabilida ya que se supoe de cada resultado que sea igualmente posible.
Dice que si hay x posibles resultados favorables a la ocurrencia de un evento A y z posibles resultados desfavorables a la ocurrencia de A, y todos los resultados son igualmente posibles y mutuamente excluyente (no pueden ocurrir los dos al mismo tiempo), entonces la probabilidad de que ocurra A es:

El enfoque clásico de la probabilidad se basa en la suposición de que cada resultado sea igualmente posible.
Este enfoque es llamado enfoque a priori porque permite, (en caso de que pueda aplicarse) calcular el valor de probabilidad antes de observar cualquier evento de muestra.
Ejemplo:
Si tenemos en una caja 15 piedras verdes y 9 piedras rojas. La probabilidad de sacar una piedra roja en un intento es:
COMENTARIO: estos nos indica que todos los eventos propramados o planteados tiene la misma probabilida ya que se supoe de cada resultado que sea igualmente posible.
PROBABILIDAD OBJETIVA:
PROBABILIDAD OBJETIVA
Aquella que se determina tomando como base algún criterio experimental u objetivo ajeno al sujeto deci-sor, como el cociente entre el número de casos favorables y número de casos posibles o el límite de una frecuencia relativa. Incluso en estos casos la determinación de la probabilidad entraña un cierto grado de subjetividad. Por ejemplo, cuando al lanzar un dado se le atribuye a la cara seis 1/6 de probabilidad se está suponiendo implícitamente que el dado está perfectamente construido.
La toma de decisiones es el proceso mediante el cual se realiza una elección entre las alternativas o formas para resolver diferentes situaciones de la vida, estas se pueden presentar en diferentes contextos: a nivel laboral, familiar, sentimental, empresarial, etc., es decir, en todo momento se toman decisiones, la diferencia entre cada una de estas es el proceso o la forma en la cual se llega a ellas. La toma de decisiones consiste, básicamente, en elegir una alternativa entre las disponibles, a los efectos de resolver un problema actual o potencial, (aún cuando no se evidencie un conflicto latente).
La toma de decisiones a nivel individual es caracterizada por que una persona haga uso de su razonamiento y pensamiento para elegir una decisión a un problema que se le presente en la vida; es decir, si una persona tiene un problema, ésta deberá ser capaz de resolverlo individualmente a través de tomar decisiones con ese especifico motivo. En la toma de decisiones importa la elección de un camino a seguir, por lo que en un estadio anterior deben evaluarse alternativas de acción. Si estas últimas no están presentes, no existirá decisión.
Para tomar una decisión, no importa su naturaleza, es necesario conocer, comprender, analizar un problema, para así poder darle solución; en algunos casos por ser tan simples y cotidianos, este proceso se realiza de forma implícita y se soluciona muy rápidamente, pero existen otros casos en los cuales las consecuencias de una mala o buena elección puede tener repercusiones en la vida y si es en un contexto laboral en el éxito o fracaso de la organizacion, para los cuales es necesario realizar un proceso más estructurado que puede dar más seguridad e información para resolver el problema. Las decisiones nos atañen a todos ya que gracias a ellas podemos tener una opinión crítica.
Toda mala decisión que tomo va seguida de otra mala decisión.
COMENTARIO:
Esto nos indica que todos los eventos tienen la misma probabilidad y se soluciona muy ràpidamente ya sea mala o buena consecuencia.
Aquella que se determina tomando como base algún criterio experimental u objetivo ajeno al sujeto deci-sor, como el cociente entre el número de casos favorables y número de casos posibles o el límite de una frecuencia relativa. Incluso en estos casos la determinación de la probabilidad entraña un cierto grado de subjetividad. Por ejemplo, cuando al lanzar un dado se le atribuye a la cara seis 1/6 de probabilidad se está suponiendo implícitamente que el dado está perfectamente construido.
La toma de decisiones es el proceso mediante el cual se realiza una elección entre las alternativas o formas para resolver diferentes situaciones de la vida, estas se pueden presentar en diferentes contextos: a nivel laboral, familiar, sentimental, empresarial, etc., es decir, en todo momento se toman decisiones, la diferencia entre cada una de estas es el proceso o la forma en la cual se llega a ellas. La toma de decisiones consiste, básicamente, en elegir una alternativa entre las disponibles, a los efectos de resolver un problema actual o potencial, (aún cuando no se evidencie un conflicto latente).
La toma de decisiones a nivel individual es caracterizada por que una persona haga uso de su razonamiento y pensamiento para elegir una decisión a un problema que se le presente en la vida; es decir, si una persona tiene un problema, ésta deberá ser capaz de resolverlo individualmente a través de tomar decisiones con ese especifico motivo. En la toma de decisiones importa la elección de un camino a seguir, por lo que en un estadio anterior deben evaluarse alternativas de acción. Si estas últimas no están presentes, no existirá decisión.
Para tomar una decisión, no importa su naturaleza, es necesario conocer, comprender, analizar un problema, para así poder darle solución; en algunos casos por ser tan simples y cotidianos, este proceso se realiza de forma implícita y se soluciona muy rápidamente, pero existen otros casos en los cuales las consecuencias de una mala o buena elección puede tener repercusiones en la vida y si es en un contexto laboral en el éxito o fracaso de la organizacion, para los cuales es necesario realizar un proceso más estructurado que puede dar más seguridad e información para resolver el problema. Las decisiones nos atañen a todos ya que gracias a ellas podemos tener una opinión crítica.
Toda mala decisión que tomo va seguida de otra mala decisión.
COMENTARIO:
Esto nos indica que todos los eventos tienen la misma probabilidad y se soluciona muy ràpidamente ya sea mala o buena consecuencia.
ESPERZANZA MATEMATICA:
Esperanza matemática
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Definición [editar]
Para una variable aleatoria discreta con valores posibles y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
Para una variable aleatoria continua la esperanza se calcula mediante la integral de todos los valores y la función de densidad :
o
La esperanza también se suele simbolizar con
Las esperanzas para se llaman momentos de orden . Más importantes son los momentos centrados .
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.
Propiedades [editar]
La esperanza es un operador lineal, ya que:
Combinando estas propiedades, podemos ver que -
donde e son variables aleatorias y y dos constantes cualesquiera.
COMENTARIO:
esto nos indica que los resultados posibles asi como las probabilidades de que ocurren cada uno de ellos, que de un numero exacto como se opera bueno en primer lugar si se trata de ganar se suma pero de lo contrario se le resta la cantidad planteada, por ejemplo 1er. si el resultado es de 500 y la probabilidad es de 0.15 esas dos cantidades se multiplica y luego se usa el signo mas si se trata de ganar pero si se trata de perder entonces se le resta dicha cantidad y asi sucesivamente obtener un nùmero o dato exacto de lo que queremos determinar.
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Definición [editar]
Para una variable aleatoria discreta con valores posibles y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
Para una variable aleatoria continua la esperanza se calcula mediante la integral de todos los valores y la función de densidad :
o
La esperanza también se suele simbolizar con
Las esperanzas para se llaman momentos de orden . Más importantes son los momentos centrados .
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.
Propiedades [editar]
La esperanza es un operador lineal, ya que:
Combinando estas propiedades, podemos ver que -
donde e son variables aleatorias y y dos constantes cualesquiera.
COMENTARIO:
esto nos indica que los resultados posibles asi como las probabilidades de que ocurren cada uno de ellos, que de un numero exacto como se opera bueno en primer lugar si se trata de ganar se suma pero de lo contrario se le resta la cantidad planteada, por ejemplo 1er. si el resultado es de 500 y la probabilidad es de 0.15 esas dos cantidades se multiplica y luego se usa el signo mas si se trata de ganar pero si se trata de perder entonces se le resta dicha cantidad y asi sucesivamente obtener un nùmero o dato exacto de lo que queremos determinar.
COMENTARIO :
Un àrbol de probabilidad es una grafica que representa los resiltados posibles de un evento asi como la probabilidad de ocurrencia. ya que por medio de ella nos facilita identifar los eventos que queremos realizar de una manera eficiente y clara.
ARBOL DE PROBABILIDAD.
Consideremos ahora el siguiente experimento : Dos urnas, A y B ,la urna A, contiene 3 bolas verdes y 2 bolas rojas, la urna B contiene 2 bolas verdes y 3 bolas rojas.
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de experimentos, se realiza un esquema, llamado : árbol de probabilidades
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de experimentos, se realiza un esquema, llamado : árbol de probabilidades

ARBOL DE PROBABILIDA
Consideremos ahora el siguiente experimento : Dos urnas, A y B ,la urna A, contiene 3 bolas verdes y 2 bolas rojas, la urna B contiene 2 bolas verdes y 3 bolas rojas.
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de exp erimentos, se realiza un esquema, llamado : árbol de probabilidades
erimentos, se realiza un esquema, llamado : árbol de probabilidades
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de exp
 erimentos, se realiza un esquema, llamado : árbol de probabilidades
erimentos, se realiza un esquema, llamado : árbol de probabilidades
Suscribirse a:
Entradas (Atom)
