BUENO APROVECHANDO ESTE ESPACIO PARA PODER EXPRESAR MIS IDEAS, Y MI PUNTO DE VISTA A CERCA DEL SISTEMA EN EL CURSO, QUE FUE RECAVADO ESTE AÑO CORRIENTE, PARA MI ES UN GUSTO LLENAR ESTAS LINEAS, EXCELENTE IDEA, Y EN REALIDAD, NINGUN CATEDRÁTICO NOS LO DA LA OPORTUNIDAD DE EXPRESAR NUESTRO PUNTO DE VISTA ACERCA DE LA ENSEÑANZA QUE NOS IMPARTEN LOS DOCENTES DEL COLEGIO...
ESTADÍSTICA ES UN CURSO DE MUCHO INTERES PARA ALUMNOS QUE ESTUDIA PARA PERITO EN ADMÓN DE EMPRESAS, YA QUE DE ELLA LOGRAMOS TENER BUENOS CONOCIMIENTOS EN LA ENSEÑANZA ACADEMIA, INCLULYENDO EL CATEDRÁTICO IMPARTIÓ LO MEJOR PARA NOSOTROS, (as) PARA QUE SE NOS HAGA FÁCIL LLEGAR A LA UNIVERSIDAD, SIN NINGUN PROBLEMA EN LO QUE ES EL CONOCIMIENTO DE TRABAJOS VIRTUALES, MANUALES . YA QUE REALIZAMOS DISTINTAS ACTIVIDADES QUE NOS HIZO DESPERTAR EN NUESTRA INGNORANCIA, QUE BUENO FUERA QUE TODOS LOS CATEDRÁTICOS FUERAN ASI COMO EL PROF. CHAVARRÍA NO TENGO NINGUN COMENTARIO NEGATIVO HACIA EL, YA QUE SE NOTA QUE DOMINA SUS DEMÁS COMPAÑEROS DOCENTES... TE FELICITO PROFE.
jueves, 2 de octubre de 2008
opinion acerca del curso
BUENO ANTES QUE NADA TE FELICITO PROFESOR POR HABERNOS EXIGIDO TRABAJANDO BAJO PRESION A MI PUNTO DE VISTA QUE CON EL AÑO QUE ESTAMOS YA PARA CULMINAR HE APRENDIDO BASTANTE CONOCIMIENTOS AVANZADOS, EN LA ENSEÑANZA, BUENO SE NOTA QUE EL ESTUDIANTE A DADO LO MEJOR PARA REALIZAR CADA ACTIVIDAD, AUNQUE TALVES PARA ALGUNOS FUE UN POCO DIFICIL PERO IGUAL MANERA DIMOS NUESTRA DEDICACION Y ESFUERZO PARA PODER DOMINAR LOS TEMAS QUE SE VIERON EN CLASES ...Y ANTE MANO GRACIAS POR TERNERNOS PACIENCIA EN LO QUE EL ACTITUDINAL, SIGUE ADELANTE PROFESOR, LO FELICITO POR SER UN EXCELENTE CATEDRÁTICO...GRACIAS POR LA ENSEÑANZA QUE DIOS TE BENDIGA... HOY Y SIEMPRE....
lunes, 29 de septiembre de 2008
viernes, 26 de septiembre de 2008
SUCESOS MUTUAMENTE EXCLUYENTES:
Exclulir significa "dejar fuera", de manera que dos sucesos seràn excluyentes si ellos no tienen elementos comunes (es decir uno excluye al otro).
COMENTARIO:
Es decir, que la intersección de ambos eventos es vacía. Si dos o más eventos no pueden ocurrir simultáneamente.
COMENTARIO:
Es decir, que la intersección de ambos eventos es vacía. Si dos o más eventos no pueden ocurrir simultáneamente.
AXIOMAS:
Un axioma es el elemento bàsico de un sistema de lògica formal y junto con las reglas de inferencia definen un sistema deductivo.
La palabra axioma proviene del griego αξιωμα (axioma), que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba.
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada.Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.
La probabilidad P de un suceso E, denotada por P(E), se define con respecto a un "universo" o espacio muestral Ω, conjunto de todos los posibles sucesos elementales, tal que P verifique los Axiomas de Kolmogórov, enunciados por el matemático ruso de este nombre en 1933. En este sentido, el suceso E es, en términos matemáticos, un subconjunto de Ω.
COMENTARIO:
Es una gramàtica formal capaz de representar cierto aspecto de la realidad.sin necesidad de demostraciòn es aquella que se considera verdadera sin ninguna necesidad de prueba. Es una forma de expresar lògicamente para llegar a una conclusiòn, que se clasifica en dos aspectos importantes las cuales se menciona; Axiomas lògicos: que son verdaderos en cualquier universo posible. Y se darà a conocer su fòrmula respectiva.
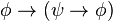


Los Axiomas no-lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo naturales, los axiomas no-lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no-lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no-lógicos es postulado.
Los axiomas no-lógicos esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aún sin la introducción de este axioma se puede desarrollar la terìa de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
La palabra axioma proviene del griego αξιωμα (axioma), que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba.
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada.Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función que definimos sobre unos sucesos determine consistentemente valores de probabilidad sobre dichos sucesos.
La probabilidad P de un suceso E, denotada por P(E), se define con respecto a un "universo" o espacio muestral Ω, conjunto de todos los posibles sucesos elementales, tal que P verifique los Axiomas de Kolmogórov, enunciados por el matemático ruso de este nombre en 1933. En este sentido, el suceso E es, en términos matemáticos, un subconjunto de Ω.
COMENTARIO:
Es una gramàtica formal capaz de representar cierto aspecto de la realidad.sin necesidad de demostraciòn es aquella que se considera verdadera sin ninguna necesidad de prueba. Es una forma de expresar lògicamente para llegar a una conclusiòn, que se clasifica en dos aspectos importantes las cuales se menciona; Axiomas lògicos: que son verdaderos en cualquier universo posible. Y se darà a conocer su fòrmula respectiva.
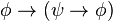


Los Axiomas no-lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo naturales, los axiomas no-lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no-lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no-lógicos es postulado.
Los axiomas no-lógicos esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aún sin la introducción de este axioma se puede desarrollar la terìa de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
ESPERANZA MATEMÀTICA:
Una definición fácil de entender de lo que aquí llamaremos «Esperanza Matemática» es la relación entre el premio obtenido y probabilidad de acertar.
La definición matemática de «Esperanza Matemática» o Valor Esperado es bastante más compleja, pero en el desarrollo de este Sistema se limita a Premio x Probabilidad. Aquí, un valor para la esperanza matemática de 1 indica «juego justo», un «menor que uno» indica «desfavorable para el jugador» y un «mayor que uno» es «favorable para el jugador» ( en las definiciones formales el cero suele ser el «juego justo», y los valores negativos o positivos indican «positivo o negativo para el jugador»).
Si la esperanza matemática es 1, el juego es «justo». Por ejemplo, apostar 1 euro a que una moneda sale cara o cruz, si el premio por acertar son 2 euros, y si se pierde, 0 euros. La esperanza del juego es 2 · (1/2) = 1. Entonces, consecuentemente con la teoría de juegos, podría pagar el euro para jugar o para rechazar jugar, porque de cualquier manera su expectativa total sería 0.
Si la esperanza matemática es menor que 1, el juego es «desfavorable para el jugador». Un sorteo que pague 500 a 1 pero en el que la probabilidad de acertar sea de 1 entre 1.000, la esperanza matemática es 500 · (1/1.000) = 0,5.
Si la esperanza matemática es mayor que 1, el juego es «favorable para el jugador», todo un «chollo» para el jugador. Un ejemplo sería un juego en el que se paga 10 a 1 por acertar el número que va a salir en un dado, en donde hay una probabilidad de acertar es de 1 entre 6. En este ejemplo el valor de la esperanza matemática es 10 · (1/6)=1,67 y por tanto en esas condiciones es juego «beneficioso» para el jugador.
Esperanza matemática de las loterías
La esperanza matemática es un valor importante que conocer para cualquier tipo de premio, en función de su dificultad, y para cada sorteo concreto.
En la Primitiva, la esperanza matemática general o promedio es sencillamente 0,55 y en Euromillones es 0,5. Se corresponde a la cantidad que se devuelve en premios: el 55% o el 50% del total apostado por los jugadores. Ese dinero siempre se devuelve, teniendo en cuenta que con el tiempo los premios no entregados se acumulan en Botes.
En la Primitiva el reparto de premios funciona de modo que la cantidad jugada por todos los jugadores (excepto el 45% que se queda la organización) se suma y reparte en diversas categorías: una parte para los de más aciertos, otra parte para premios menores, reintegros, etc. Esto marca ciertamente diferencias entre la esperanza matemática (premios por probabilidad) de las diferentes categorías de premios. La esperanza matemática más alta es la del Reintegro que es de 0,1 (10 %).
Estos cálculos, que de por sí son sencillos, se ven complicados por algunas reglas relativamente recientes, como el «premio fijo para los acertantes de 3» o «los acertantes de 5 nunca pueden ganar más que los de 6», pero son en cualquier caso calculables con precisión.
En general, y para la Loto tradicional la norma a grandes rasgos es que la esperanza matemática es mayor que 1 cuando la cantidad de premios total (el bote más el 55% de la cantidad que todos los jugadores apuestan ese día) es mayor de lo que valen 13,9 millones de apuestas (dado que la probabilidad de acertar es de 1 entre 13,9 millones) y esto ocurre en muy muy muy raras ocasiones.
Pero imagenemos como hipótesis de trabajo que llega un día en el que se ha acumulado un bote de 20 millones de euros y en el que por alguna circunstancia nadie juega a la Loto excepto una persona. A 1 euro por apuesta, esto supondría pagar unos 14 millones de euros para jugar a todas las combinaciones y embolsarse todos los premios: el bote más lógicamente la recuperación del 55% de lo apostado y un 10% en reintegros (7,7 millones de euros, correspondiente al resto de premios menores de 5, 4, reintegros, etc.) Resultado: apostando 14 millones se recuperarían 27,7 millones de euros. Casi otros 14 millones de beneficio. ¡Buen negocio!
Un ejemplo real fue el sorteo de Bonoloto (Loto 6/49) del 18/11/1990. Un bote de 1.151 millones de pesetas se sumó a una recaudación de sólo 374 millones. A 25 pesetas por apuesta se hicieron en total unos 15 millones de apuestas. La probabilidad de acertar 6 era de 1 entre 14 millones, como siempre (y en total se repartía el 55% de la recaudación, como siempre). El premio de 1.200 millones que recibió un único acertante de 6 números tenía como base una esperanza matemática de 3,2 (frente a 1 que sería lo normal en un “juego justo” o 0,55 en un día convencional sin bote). Es decir, si el juego hubiera sido “justo” tanto para el jugador como para la banca, el premio debería haber sido de sólo unos 350 millones. Pero el ganador se llevó 1.200 millones porque había un bote acumulado de muchísimas semanas. La esperanza matemática promedio de ese día, contando todos los premios, era de 3,6. ¡Ese día ciertamente era mejor jugar a la Loto que no jugar!
Casi siempre, cualquier juego real de apuestas tiene esperanza menor que 1: lo más probable es perder dinero. El motivo por el que se juega es que en caso de ganar, los premios son de escándalo. Estamos dispuestos a perder una cantidad pequeña de dinero casi con seguridad a cambio de la posibilidad, por pequeña que sea, de hacernos ricos de la noche a la mañana.
COMENTARIO:
Es aquella que asume diferentes valores a consecuencia de los resultados de un experimento aleatorio que es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. al igual nos ayuda a describir la tendencia, dispersiòn, asimetrìa, y apuntamiento de sus valores tales puede ser el consepto fundamental en el estudio de las distribuciones de probabilidad. En la cual se menciona la desviaciòn estàndar, los cuartiles, la asimetrìa que abarca de una funciòn numèrica que define la probabilidad de un conjunto dado. Esto es el mas comùn promedio utilizado. ya que para obtener el valor esperado se opera multiplicando cada valor que asume la probabilidad, de ocurrencia de ese valor y luego lo sumamos los productos. Que es un promedio de los resultados que se esperan en el futuro.
La definición matemática de «Esperanza Matemática» o Valor Esperado es bastante más compleja, pero en el desarrollo de este Sistema se limita a Premio x Probabilidad. Aquí, un valor para la esperanza matemática de 1 indica «juego justo», un «menor que uno» indica «desfavorable para el jugador» y un «mayor que uno» es «favorable para el jugador» ( en las definiciones formales el cero suele ser el «juego justo», y los valores negativos o positivos indican «positivo o negativo para el jugador»).
Si la esperanza matemática es 1, el juego es «justo». Por ejemplo, apostar 1 euro a que una moneda sale cara o cruz, si el premio por acertar son 2 euros, y si se pierde, 0 euros. La esperanza del juego es 2 · (1/2) = 1. Entonces, consecuentemente con la teoría de juegos, podría pagar el euro para jugar o para rechazar jugar, porque de cualquier manera su expectativa total sería 0.
Si la esperanza matemática es menor que 1, el juego es «desfavorable para el jugador». Un sorteo que pague 500 a 1 pero en el que la probabilidad de acertar sea de 1 entre 1.000, la esperanza matemática es 500 · (1/1.000) = 0,5.
Si la esperanza matemática es mayor que 1, el juego es «favorable para el jugador», todo un «chollo» para el jugador. Un ejemplo sería un juego en el que se paga 10 a 1 por acertar el número que va a salir en un dado, en donde hay una probabilidad de acertar es de 1 entre 6. En este ejemplo el valor de la esperanza matemática es 10 · (1/6)=1,67 y por tanto en esas condiciones es juego «beneficioso» para el jugador.
Esperanza matemática de las loterías
La esperanza matemática es un valor importante que conocer para cualquier tipo de premio, en función de su dificultad, y para cada sorteo concreto.
En la Primitiva, la esperanza matemática general o promedio es sencillamente 0,55 y en Euromillones es 0,5. Se corresponde a la cantidad que se devuelve en premios: el 55% o el 50% del total apostado por los jugadores. Ese dinero siempre se devuelve, teniendo en cuenta que con el tiempo los premios no entregados se acumulan en Botes.
En la Primitiva el reparto de premios funciona de modo que la cantidad jugada por todos los jugadores (excepto el 45% que se queda la organización) se suma y reparte en diversas categorías: una parte para los de más aciertos, otra parte para premios menores, reintegros, etc. Esto marca ciertamente diferencias entre la esperanza matemática (premios por probabilidad) de las diferentes categorías de premios. La esperanza matemática más alta es la del Reintegro que es de 0,1 (10 %).
Estos cálculos, que de por sí son sencillos, se ven complicados por algunas reglas relativamente recientes, como el «premio fijo para los acertantes de 3» o «los acertantes de 5 nunca pueden ganar más que los de 6», pero son en cualquier caso calculables con precisión.
En general, y para la Loto tradicional la norma a grandes rasgos es que la esperanza matemática es mayor que 1 cuando la cantidad de premios total (el bote más el 55% de la cantidad que todos los jugadores apuestan ese día) es mayor de lo que valen 13,9 millones de apuestas (dado que la probabilidad de acertar es de 1 entre 13,9 millones) y esto ocurre en muy muy muy raras ocasiones.
Pero imagenemos como hipótesis de trabajo que llega un día en el que se ha acumulado un bote de 20 millones de euros y en el que por alguna circunstancia nadie juega a la Loto excepto una persona. A 1 euro por apuesta, esto supondría pagar unos 14 millones de euros para jugar a todas las combinaciones y embolsarse todos los premios: el bote más lógicamente la recuperación del 55% de lo apostado y un 10% en reintegros (7,7 millones de euros, correspondiente al resto de premios menores de 5, 4, reintegros, etc.) Resultado: apostando 14 millones se recuperarían 27,7 millones de euros. Casi otros 14 millones de beneficio. ¡Buen negocio!
Un ejemplo real fue el sorteo de Bonoloto (Loto 6/49) del 18/11/1990. Un bote de 1.151 millones de pesetas se sumó a una recaudación de sólo 374 millones. A 25 pesetas por apuesta se hicieron en total unos 15 millones de apuestas. La probabilidad de acertar 6 era de 1 entre 14 millones, como siempre (y en total se repartía el 55% de la recaudación, como siempre). El premio de 1.200 millones que recibió un único acertante de 6 números tenía como base una esperanza matemática de 3,2 (frente a 1 que sería lo normal en un “juego justo” o 0,55 en un día convencional sin bote). Es decir, si el juego hubiera sido “justo” tanto para el jugador como para la banca, el premio debería haber sido de sólo unos 350 millones. Pero el ganador se llevó 1.200 millones porque había un bote acumulado de muchísimas semanas. La esperanza matemática promedio de ese día, contando todos los premios, era de 3,6. ¡Ese día ciertamente era mejor jugar a la Loto que no jugar!
Casi siempre, cualquier juego real de apuestas tiene esperanza menor que 1: lo más probable es perder dinero. El motivo por el que se juega es que en caso de ganar, los premios son de escándalo. Estamos dispuestos a perder una cantidad pequeña de dinero casi con seguridad a cambio de la posibilidad, por pequeña que sea, de hacernos ricos de la noche a la mañana.
COMENTARIO:
Es aquella que asume diferentes valores a consecuencia de los resultados de un experimento aleatorio que es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. al igual nos ayuda a describir la tendencia, dispersiòn, asimetrìa, y apuntamiento de sus valores tales puede ser el consepto fundamental en el estudio de las distribuciones de probabilidad. En la cual se menciona la desviaciòn estàndar, los cuartiles, la asimetrìa que abarca de una funciòn numèrica que define la probabilidad de un conjunto dado. Esto es el mas comùn promedio utilizado. ya que para obtener el valor esperado se opera multiplicando cada valor que asume la probabilidad, de ocurrencia de ese valor y luego lo sumamos los productos. Que es un promedio de los resultados que se esperan en el futuro.
jueves, 25 de septiembre de 2008
RESULTADO:
Resultado. Es una consecuencia particular de un experimento.
COMENTARIO: esto nos señala de que debemos de encontrar la lògica de lo que queremos obtener de un eventos experimentado. o ya sea obteniendo datos exactos de una operacion de eventos ocurrentes.
COMENTARIO: esto nos señala de que debemos de encontrar la lògica de lo que queremos obtener de un eventos experimentado. o ya sea obteniendo datos exactos de una operacion de eventos ocurrentes.
EXPERIMENTOS:
Experimento. Es un proceso que lleva a la ocurrencia de una y sólo una de varias observaciones posibles.
COMENTARIO:
es cuando observamos un suceso y atravès de ellas encontramos posibles resultados por la cual queremos llegar a conocer.
COMENTARIO:
es cuando observamos un suceso y atravès de ellas encontramos posibles resultados por la cual queremos llegar a conocer.
LA PROBABILIDAD:
Probabilidad. Es un valor entre uno y cero, inclusive, que describe la posibilidad de que ocurra un resultado o evento determinado como consecuencia de la realización de un experimento
COMENTARIO:
Por medio de ella nos permite describir la posibilidad de que ocurra un resultado de dicho proceso que conlleva a la ocurrencia de una o varias observaciones posibles.
COMENTARIO:
Por medio de ella nos permite describir la posibilidad de que ocurra un resultado de dicho proceso que conlleva a la ocurrencia de una o varias observaciones posibles.
Reglas de Multiplicación
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
Los valores de los parámetros de la distribución de probabilidad normal son = 0 y = 1. Cualquier conjunto de valores X normalmente distribuido pueden convertirse en valores normales estándar z por medio de la formula:
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
Los valores de los parámetros de la distribución de probabilidad normal son = 0 y = 1. Cualquier conjunto de valores X normalmente distribuido pueden convertirse en valores normales estándar z por medio de la formula:
REGLAS DE MULTIPLICACION:
Reglas de Multiplicación
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
COMENTARIO:
esto nos indica que la ocurrencia de eventos se interceda entre los conjuntos posibles y que sean independientes o dependientes y como tambien representa una muestra en la cual es una campana. y atravès de ella marca motivos distintos y bàsicamente se obtiene aproximando distribuciones de probabilidad..
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(BA) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(AB) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
COMENTARIO:
esto nos indica que la ocurrencia de eventos se interceda entre los conjuntos posibles y que sean independientes o dependientes y como tambien representa una muestra en la cual es una campana. y atravès de ella marca motivos distintos y bàsicamente se obtiene aproximando distribuciones de probabilidad..
EVENTOS DEPENDIENTES:
Eventos dependientes
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(AB) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que AB no es una fracción.
P(AB) = P(A y B)/P(B) o P(BA) = P(A y B)/P(A)
COMENTARIO:
Consiste en hallar la probabilidad de que al extraer cualquiera de ellas ambas sea de otro gènero, ya sea marcando la diferencia entre ambas.
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(AB) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que AB no es una fracción.
P(AB) = P(A y B)/P(B) o P(BA) = P(A y B)/P(A)
COMENTARIO:
Consiste en hallar la probabilidad de que al extraer cualquiera de ellas ambas sea de otro gènero, ya sea marcando la diferencia entre ambas.
EVENTOS INDEPENDIENTES:
Eventos Independientes
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Ejemplo:
lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento.
COMENTARIO:
Son eventos que se ocurre y que no depende de otros ya que una vez tomada el objeto se regresa de nuevo a la probabilidad donde se obtuvo en el caso de la moneda como se menciona anteriormente.
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Ejemplo:
lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento.
COMENTARIO:
Son eventos que se ocurre y que no depende de otros ya que una vez tomada el objeto se regresa de nuevo a la probabilidad donde se obtuvo en el caso de la moneda como se menciona anteriormente.
EL ENFOQUE SUBJETIVO:
El enfoque subjetivo
Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal.
COMENTARIO :
CONSISTE EN EVENTOS QUE OCURRE EL INDIVIDUO DEPENDE DEL NIVEL DE CREENCIA QUE TIENE QUE BASA TAMBIEN EN LO QUE ES ADECUADO CUANDO HAY SOLO UNA OPORTUNIDAD DE REALIZARLO .
Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal.
COMENTARIO :
CONSISTE EN EVENTOS QUE OCURRE EL INDIVIDUO DEPENDE DEL NIVEL DE CREENCIA QUE TIENE QUE BASA TAMBIEN EN LO QUE ES ADECUADO CUANDO HAY SOLO UNA OPORTUNIDAD DE REALIZARLO .
EL ENFOQUE DE FRECUENCIA RELATIVA:
El enfoque de frecuencia relativa
También llamado Enfoque Empírico, determina la probabilidad sobre la base de la proporción de veces que ocurre un evento favorable en un numero de observaciones. En este enfoque no ese utiliza la suposición previa de aleatoriedad. Porque la determinación de los valores de probabilidad se basa en la observación y recopilación de datos.
Ejemplo:
Se ha observado que 9 de cada 50 vehículos que pasan por una esquina no tienen cinturón de seguridad. Si un vigilante de transito se para en esa misma esquina un ida cualquiera ¿Cuál será la probabilidad de que detenga un vehículo sin cinturón de seguridad?

COMENTARIO:
ESTOS NOS INDICA QUE TIENE LÌMITE LA OBSERVACION QUE QUEREMOS REALIZAR Y TAMBIEN IMPLICA OBTENER DATOS EXACTOS. Y SE DEBE SUPONER ALEATORIAMENTE UN ENFOQUE.
También llamado Enfoque Empírico, determina la probabilidad sobre la base de la proporción de veces que ocurre un evento favorable en un numero de observaciones. En este enfoque no ese utiliza la suposición previa de aleatoriedad. Porque la determinación de los valores de probabilidad se basa en la observación y recopilación de datos.
Ejemplo:
Se ha observado que 9 de cada 50 vehículos que pasan por una esquina no tienen cinturón de seguridad. Si un vigilante de transito se para en esa misma esquina un ida cualquiera ¿Cuál será la probabilidad de que detenga un vehículo sin cinturón de seguridad?
COMENTARIO:
ESTOS NOS INDICA QUE TIENE LÌMITE LA OBSERVACION QUE QUEREMOS REALIZAR Y TAMBIEN IMPLICA OBTENER DATOS EXACTOS. Y SE DEBE SUPONER ALEATORIAMENTE UN ENFOQUE.
EL ENFOQUE CLÀSICO:
El enfoque clásico
Dice que si hay x posibles resultados favorables a la ocurrencia de un evento A y z posibles resultados desfavorables a la ocurrencia de A, y todos los resultados son igualmente posibles y mutuamente excluyente (no pueden ocurrir los dos al mismo tiempo), entonces la probabilidad de que ocurra A es:
El enfoque clásico de la probabilidad se basa en la suposición de que cada resultado sea igualmente posible.
Este enfoque es llamado enfoque a priori porque permite, (en caso de que pueda aplicarse) calcular el valor de probabilidad antes de observar cualquier evento de muestra.
Ejemplo:
Si tenemos en una caja 15 piedras verdes y 9 piedras rojas. La probabilidad de sacar una piedra roja en un intento es:

COMENTARIO: estos nos indica que todos los eventos propramados o planteados tiene la misma probabilida ya que se supoe de cada resultado que sea igualmente posible.
Dice que si hay x posibles resultados favorables a la ocurrencia de un evento A y z posibles resultados desfavorables a la ocurrencia de A, y todos los resultados son igualmente posibles y mutuamente excluyente (no pueden ocurrir los dos al mismo tiempo), entonces la probabilidad de que ocurra A es:

El enfoque clásico de la probabilidad se basa en la suposición de que cada resultado sea igualmente posible.
Este enfoque es llamado enfoque a priori porque permite, (en caso de que pueda aplicarse) calcular el valor de probabilidad antes de observar cualquier evento de muestra.
Ejemplo:
Si tenemos en una caja 15 piedras verdes y 9 piedras rojas. La probabilidad de sacar una piedra roja en un intento es:
COMENTARIO: estos nos indica que todos los eventos propramados o planteados tiene la misma probabilida ya que se supoe de cada resultado que sea igualmente posible.
PROBABILIDAD OBJETIVA:
PROBABILIDAD OBJETIVA
Aquella que se determina tomando como base algún criterio experimental u objetivo ajeno al sujeto deci-sor, como el cociente entre el número de casos favorables y número de casos posibles o el límite de una frecuencia relativa. Incluso en estos casos la determinación de la probabilidad entraña un cierto grado de subjetividad. Por ejemplo, cuando al lanzar un dado se le atribuye a la cara seis 1/6 de probabilidad se está suponiendo implícitamente que el dado está perfectamente construido.
La toma de decisiones es el proceso mediante el cual se realiza una elección entre las alternativas o formas para resolver diferentes situaciones de la vida, estas se pueden presentar en diferentes contextos: a nivel laboral, familiar, sentimental, empresarial, etc., es decir, en todo momento se toman decisiones, la diferencia entre cada una de estas es el proceso o la forma en la cual se llega a ellas. La toma de decisiones consiste, básicamente, en elegir una alternativa entre las disponibles, a los efectos de resolver un problema actual o potencial, (aún cuando no se evidencie un conflicto latente).
La toma de decisiones a nivel individual es caracterizada por que una persona haga uso de su razonamiento y pensamiento para elegir una decisión a un problema que se le presente en la vida; es decir, si una persona tiene un problema, ésta deberá ser capaz de resolverlo individualmente a través de tomar decisiones con ese especifico motivo. En la toma de decisiones importa la elección de un camino a seguir, por lo que en un estadio anterior deben evaluarse alternativas de acción. Si estas últimas no están presentes, no existirá decisión.
Para tomar una decisión, no importa su naturaleza, es necesario conocer, comprender, analizar un problema, para así poder darle solución; en algunos casos por ser tan simples y cotidianos, este proceso se realiza de forma implícita y se soluciona muy rápidamente, pero existen otros casos en los cuales las consecuencias de una mala o buena elección puede tener repercusiones en la vida y si es en un contexto laboral en el éxito o fracaso de la organizacion, para los cuales es necesario realizar un proceso más estructurado que puede dar más seguridad e información para resolver el problema. Las decisiones nos atañen a todos ya que gracias a ellas podemos tener una opinión crítica.
Toda mala decisión que tomo va seguida de otra mala decisión.
COMENTARIO:
Esto nos indica que todos los eventos tienen la misma probabilidad y se soluciona muy ràpidamente ya sea mala o buena consecuencia.
Aquella que se determina tomando como base algún criterio experimental u objetivo ajeno al sujeto deci-sor, como el cociente entre el número de casos favorables y número de casos posibles o el límite de una frecuencia relativa. Incluso en estos casos la determinación de la probabilidad entraña un cierto grado de subjetividad. Por ejemplo, cuando al lanzar un dado se le atribuye a la cara seis 1/6 de probabilidad se está suponiendo implícitamente que el dado está perfectamente construido.
La toma de decisiones es el proceso mediante el cual se realiza una elección entre las alternativas o formas para resolver diferentes situaciones de la vida, estas se pueden presentar en diferentes contextos: a nivel laboral, familiar, sentimental, empresarial, etc., es decir, en todo momento se toman decisiones, la diferencia entre cada una de estas es el proceso o la forma en la cual se llega a ellas. La toma de decisiones consiste, básicamente, en elegir una alternativa entre las disponibles, a los efectos de resolver un problema actual o potencial, (aún cuando no se evidencie un conflicto latente).
La toma de decisiones a nivel individual es caracterizada por que una persona haga uso de su razonamiento y pensamiento para elegir una decisión a un problema que se le presente en la vida; es decir, si una persona tiene un problema, ésta deberá ser capaz de resolverlo individualmente a través de tomar decisiones con ese especifico motivo. En la toma de decisiones importa la elección de un camino a seguir, por lo que en un estadio anterior deben evaluarse alternativas de acción. Si estas últimas no están presentes, no existirá decisión.
Para tomar una decisión, no importa su naturaleza, es necesario conocer, comprender, analizar un problema, para así poder darle solución; en algunos casos por ser tan simples y cotidianos, este proceso se realiza de forma implícita y se soluciona muy rápidamente, pero existen otros casos en los cuales las consecuencias de una mala o buena elección puede tener repercusiones en la vida y si es en un contexto laboral en el éxito o fracaso de la organizacion, para los cuales es necesario realizar un proceso más estructurado que puede dar más seguridad e información para resolver el problema. Las decisiones nos atañen a todos ya que gracias a ellas podemos tener una opinión crítica.
Toda mala decisión que tomo va seguida de otra mala decisión.
COMENTARIO:
Esto nos indica que todos los eventos tienen la misma probabilidad y se soluciona muy ràpidamente ya sea mala o buena consecuencia.
ESPERZANZA MATEMATICA:
Esperanza matemática
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Definición [editar]
Para una variable aleatoria discreta con valores posibles y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
Para una variable aleatoria continua la esperanza se calcula mediante la integral de todos los valores y la función de densidad :
o
La esperanza también se suele simbolizar con
Las esperanzas para se llaman momentos de orden . Más importantes son los momentos centrados .
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.
Propiedades [editar]
La esperanza es un operador lineal, ya que:
Combinando estas propiedades, podemos ver que -
donde e son variables aleatorias y y dos constantes cualesquiera.
COMENTARIO:
esto nos indica que los resultados posibles asi como las probabilidades de que ocurren cada uno de ellos, que de un numero exacto como se opera bueno en primer lugar si se trata de ganar se suma pero de lo contrario se le resta la cantidad planteada, por ejemplo 1er. si el resultado es de 500 y la probabilidad es de 0.15 esas dos cantidades se multiplica y luego se usa el signo mas si se trata de ganar pero si se trata de perder entonces se le resta dicha cantidad y asi sucesivamente obtener un nùmero o dato exacto de lo que queremos determinar.
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
En estadística la esperanza matemática (o simplemente esperanza) o valor esperado de una variable aleatoria es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso. Por ejemplo, en un juego de azar el valor esperado es el beneficio medio.
Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética.
Definición [editar]
Para una variable aleatoria discreta con valores posibles y sus probabilidades representadas por la función de masa p(xi) la esperanza se calcula como:
Para una variable aleatoria continua la esperanza se calcula mediante la integral de todos los valores y la función de densidad :
o
La esperanza también se suele simbolizar con
Las esperanzas para se llaman momentos de orden . Más importantes son los momentos centrados .
No todas las variables aleatorias tienen un valor esperado. Por ejemplo, la distribución de Cauchy no lo tiene.
Propiedades [editar]
La esperanza es un operador lineal, ya que:
Combinando estas propiedades, podemos ver que -
donde e son variables aleatorias y y dos constantes cualesquiera.
COMENTARIO:
esto nos indica que los resultados posibles asi como las probabilidades de que ocurren cada uno de ellos, que de un numero exacto como se opera bueno en primer lugar si se trata de ganar se suma pero de lo contrario se le resta la cantidad planteada, por ejemplo 1er. si el resultado es de 500 y la probabilidad es de 0.15 esas dos cantidades se multiplica y luego se usa el signo mas si se trata de ganar pero si se trata de perder entonces se le resta dicha cantidad y asi sucesivamente obtener un nùmero o dato exacto de lo que queremos determinar.
COMENTARIO :
Un àrbol de probabilidad es una grafica que representa los resiltados posibles de un evento asi como la probabilidad de ocurrencia. ya que por medio de ella nos facilita identifar los eventos que queremos realizar de una manera eficiente y clara.
ARBOL DE PROBABILIDAD.
Consideremos ahora el siguiente experimento : Dos urnas, A y B ,la urna A, contiene 3 bolas verdes y 2 bolas rojas, la urna B contiene 2 bolas verdes y 3 bolas rojas.
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de experimentos, se realiza un esquema, llamado : árbol de probabilidades
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de experimentos, se realiza un esquema, llamado : árbol de probabilidades

ARBOL DE PROBABILIDA
Consideremos ahora el siguiente experimento : Dos urnas, A y B ,la urna A, contiene 3 bolas verdes y 2 bolas rojas, la urna B contiene 2 bolas verdes y 3 bolas rojas.
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de exp erimentos, se realiza un esquema, llamado : árbol de probabilidades
erimentos, se realiza un esquema, llamado : árbol de probabilidades
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento aleatorio y posteriormente de la urna elegida se extrae una bola. Para representar, de forma muy adecuada, este tipo de exp
 erimentos, se realiza un esquema, llamado : árbol de probabilidades
erimentos, se realiza un esquema, llamado : árbol de probabilidades
viernes, 29 de agosto de 2008
COMENTARIO:
EL DIAGRAMA DE ARBOL ES HERRAMIENTA QUE NOS FACILITA FABRICAR CUALQUIER TIPO DE AGRUPACION YA SEA PERMUTACIONES Y VARIACIONES...
DIAGRAMA DE ARBOL.
I. DIAGRAMA DE ARBOL.
Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
Ejemplos:
1.Un médico general clasifica a sus pacientes de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de árbol diga en cuantas clasificaciones pueden
estar los pacientes de este médico?
N
Solución: A
A B
N
B A
B
M AB N
A
O B
A
N
F B A
B
AB
B
O A
B
Si contamos todas las ramas terminales, nos damos cuenta que el número de clasificaciones son 2 x 4 x 3 = 24 mismas que podemos enumerar;
MAN, MAA, MAB, MBN, MBA, MBB, etc, etc.
1) Dos equipos denominados A y B se disputan la final de un partido de baloncesto, aquel equipo que gane dos juegos seguidos o complete un total de tres juegos ganados será el que gane el torneo. Mediante un diagrama de árbol diga de cuantas maneras puede ser ganado este torneo,
Solución:
A = gana el equipo A
B = gana el equipo B
A
A
A A
B A
B
B B
A
A A
A
B B B
B
B
En este diagrama se muestran que hay solo diez maneras de que se gane el torneo, que se obtienen contando las ramas terminales de este diagrama de árbol, las que es posible enumerar;
AA, ABB, ABAA, ABABA, ABABB, etc, etc.
2) Un hombre tiene tiempo de jugar ruleta cinco veces como máximo, él empieza a jugar con un dólar, apuesta cada vez un dólar y puede ganar o perder en cada juego un dólar, él se va a retirar de jugar si pierde todo su dinero, si gana tres dólares (esto es si completa un total de cuatro dólares) o si completa los cinco juegos, mediante un diagrama de árbol, diga cuántas maneras hay de que se efectué el juego de este hombre.
Solución:
$4 G $4
G $3
$3 G
G P $2
P G$3
$2 P
$1 P $0
$3 G $4
$2 G
$1 G $2
G P $2
G $2
P P
$1 P $1
P $0 P $0
$0
Si contamos las ramas terminales nos daremos cuenta que hay 11 maneras de que este hombre lleve a cabo sus apuestas, en este diagrama se han representado los cinco juegos o apuestas que este hombre tiene tiempo de jugar.
Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
Ejemplos:
1.Un médico general clasifica a sus pacientes de acuerdo a: su sexo (masculino o femenino), tipo de sangre (A, B, AB u O) y en cuanto a la presión sanguínea (Normal, Alta o Baja). Mediante un diagrama de árbol diga en cuantas clasificaciones pueden
estar los pacientes de este médico?
N
Solución: A
A B
N
B A
B
M AB N
A
O B
A
N
F B A
B
AB
B
O A
B
Si contamos todas las ramas terminales, nos damos cuenta que el número de clasificaciones son 2 x 4 x 3 = 24 mismas que podemos enumerar;
MAN, MAA, MAB, MBN, MBA, MBB, etc, etc.
1) Dos equipos denominados A y B se disputan la final de un partido de baloncesto, aquel equipo que gane dos juegos seguidos o complete un total de tres juegos ganados será el que gane el torneo. Mediante un diagrama de árbol diga de cuantas maneras puede ser ganado este torneo,
Solución:
A = gana el equipo A
B = gana el equipo B
A
A
A A
B A
B
B B
A
A A
A
B B B
B
B
En este diagrama se muestran que hay solo diez maneras de que se gane el torneo, que se obtienen contando las ramas terminales de este diagrama de árbol, las que es posible enumerar;
AA, ABB, ABAA, ABABA, ABABB, etc, etc.
2) Un hombre tiene tiempo de jugar ruleta cinco veces como máximo, él empieza a jugar con un dólar, apuesta cada vez un dólar y puede ganar o perder en cada juego un dólar, él se va a retirar de jugar si pierde todo su dinero, si gana tres dólares (esto es si completa un total de cuatro dólares) o si completa los cinco juegos, mediante un diagrama de árbol, diga cuántas maneras hay de que se efectué el juego de este hombre.
Solución:
$4 G $4
G $3
$3 G
G P $2
P G$3
$2 P
$1 P $0
$3 G $4
$2 G
$1 G $2
G P $2
G $2
P P
$1 P $1
P $0 P $0
$0
Si contamos las ramas terminales nos daremos cuenta que hay 11 maneras de que este hombre lleve a cabo sus apuestas, en este diagrama se han representado los cinco juegos o apuestas que este hombre tiene tiempo de jugar.
COMENTARIO:
son problemads que relacionan dos conjuntos mediante operaciones de uniòn, intersecciòn y diferencia. permite obtener datos que tienen relaciòn con los conjuntos dados...
TEORIA DE CONTEO:
TEORÍAS DE CONTEO
Permutaciones y combinaciones: Contar el número de eventos que cumplen con algún conjunto de condiciones. Sirven para calcular la probabilidad de un evento cuando el número de eventos posibles es muy grande.
Factoriales: Dado un número entero positivo n el producto de todos los enteros desde n hasta 1 se llama factorial de n y se denota como n!. Ejemplo:
5! = 5 * 4 * 3 * 2 * 1
en notación: n! = n * (n-1) * (n-2) * ... 1
por definición 0! = 1
otra notación: 5! = 5 * 4!
n! = n (n-l)
Los factoriales sc usan para saber el número de formas en que se pueden organizar los objetos. Ejemplo:
cuatro envases con medio de cultivo y en cada uno de ellos se incuba un organismo diferente. ¿En cuantas formas se pueden acomodar en una incubadora?
4! =4 3 * 2 * 1 = 24 maneras
Para saber cuales son las formas de colocarlos se realiza un diagrama de árbol (ver Diagrama 1).
Permutaciones y combinaciones: Contar el número de eventos que cumplen con algún conjunto de condiciones. Sirven para calcular la probabilidad de un evento cuando el número de eventos posibles es muy grande.
Factoriales: Dado un número entero positivo n el producto de todos los enteros desde n hasta 1 se llama factorial de n y se denota como n!. Ejemplo:
5! = 5 * 4 * 3 * 2 * 1
en notación: n! = n * (n-1) * (n-2) * ... 1
por definición 0! = 1
otra notación: 5! = 5 * 4!
n! = n (n-l)
Los factoriales sc usan para saber el número de formas en que se pueden organizar los objetos. Ejemplo:
cuatro envases con medio de cultivo y en cada uno de ellos se incuba un organismo diferente. ¿En cuantas formas se pueden acomodar en una incubadora?
4! =4 3 * 2 * 1 = 24 maneras
Para saber cuales son las formas de colocarlos se realiza un diagrama de árbol (ver Diagrama 1).
COMENTARIO :
LA PERMUTACIÒN ES TODO ARREGLO DE ELEMENTOS EN DONDE NOS INTERESA EL LUGAR O POSICIÒN QUE OCUPA CADA UNO DE LOS ELEMENTOS QUE CONSTITUYE DICHO ARREGLO PARA PODER VER DE UNA MANERA OBJETIVA LA DIFERENCIA ENTRE UNA COMBINACIÒN Y UNA PERMUTACIÒN...
PERMUTACIONES:
Permutaciones
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
Una permutación es una combinación en donde el orden es importante. La notación para permutaciones es P(n,r) que es la cantidad de permutaciones de “n” elementos si solamente se seleccionan “r”.
Ejemplo: Si nueve estudiantes toman un examen y todos obtienen diferente calificación, cualquier alumno podría alcanzar la calificación más alta. La segunda calificación más alta podría ser obtenida por uno de los 8 restantes. La tercera calificación podría ser obtenida por uno de los 7 restantes.
La cantidad de permutaciones posibles sería: P(9,3) = 9*8*7 = 504 combinaciones posibles de las tres calificaciones más altas.
COMENTARIO A CERCA DE LA COMBINACIÒN:
ES UNA FORMA DE AGRUPAR LOS ELEMENTOS DE UN CONJUNTO RELATIVAMENTE LARGA DE MOVIMIENTOS ES CAMBIADA DE ACUERDO AL ELEMENTO QUE COMPONE LA CAJA YA QUE TODOS LOS ELEMENTOS QUE CONTIENE SE PUEDE CUANTIFICAR, TOMANDO EN CUENTA QUE NO IMPORTA EL ORDEN EN QUE SE COLOCAN Y AL FINAL DA UN NÙMERO DE TALES COMBINACIONES...
COMBINACIÒN:
COMBINACIONES
Las combinaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
NO influye el orden en que se colocan.
Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Existen dos tipos: combinaciones sin repetición y combinaciones con repetición, cuyos símbolos son los siguientes. .
Las combinaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
NO influye el orden en que se colocan.
Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Existen dos tipos: combinaciones sin repetición y combinaciones con repetición, cuyos símbolos son los siguientes. .
jueves, 21 de agosto de 2008
EXPERIMENTOS ALEATORIOS...
4.4 Experimentos y sucesos aleatorios
Diremos que un experimento es aleatorio si se verifican las siguientes condiciones:
1.
Se puede repetir indefinidamente, siempre en las mismas condiciones;
2.
Antes de realizarlo, no se puede predecir el resultado que se va a obtener;
3.
El resultado que se obtenga, e, pertenece a un conjunto conocido previamente de resultados posibles. A este conjunto, de resultados posibles, lo denominaremos espacio muestral y lo denotaremos normalmente mediante la letra E. Los elementos del espacio muestral se denominan sucesos elementales.
Cualquier subconjunto de E será denominado suceso aleatorio, y se denotará normalmente con las letras A, B,...
Obsérvese que los sucesos elementales son sucesos aleatorios compuestos por un sólo elemento. Por supuesto los sucesos aleatorios son más generales que los elementales, ya que son conjuntos que pueden contener no a uno sólo, sino a una infinidad de sucesos elementales --y también no contener ninguno.-- Sucesos aleatorios que aparecen con gran frecuencia en el cálculo de probabilidades son los siguientes:
4.4.0.0.0.1 Suceso seguro: Es aquel que siempre se verifica después del experimento aleatorio, es decir, el mismo E
4.4.0.0.0.2 Suceso imposible: Es aquel que nunca se verifica como resultado del experimento aleatorio. Como debe ser un subconjunto de E, la única posibilidad es que el suceso imposible sea el conjunto vacío
4.4.0.0.0.3 Suceso contrario a un suceso A: También se denomina complementario de A y es el suceso que se verifica si, como resultado del experimento aleatorio, no se verifica A. Se acostumbra a denotar con el símbolo
Figura: Representación gráfica de un suceso aleatorio , y de su suceso contrario
4.4.0.1 Ejemplo Si realizamos el experimento aleatorio de lanzar un dado al aire, tenemos:
SUCESO ELEMENTALES:.......1,2,3,4,5,6
ESPACIO MUESTRAL:.........E= {,2,3,4,5,6}
SUCESOS ALEATORIOS........{0 ucesos imposibles.
E sucesos seguros
{1,2,3}
{4,5}
{2,4,6}= ---------
{1,2,3}
Diremos que un experimento es aleatorio si se verifican las siguientes condiciones:
1.
Se puede repetir indefinidamente, siempre en las mismas condiciones;
2.
Antes de realizarlo, no se puede predecir el resultado que se va a obtener;
3.
El resultado que se obtenga, e, pertenece a un conjunto conocido previamente de resultados posibles. A este conjunto, de resultados posibles, lo denominaremos espacio muestral y lo denotaremos normalmente mediante la letra E. Los elementos del espacio muestral se denominan sucesos elementales.
Cualquier subconjunto de E será denominado suceso aleatorio, y se denotará normalmente con las letras A, B,...
Obsérvese que los sucesos elementales son sucesos aleatorios compuestos por un sólo elemento. Por supuesto los sucesos aleatorios son más generales que los elementales, ya que son conjuntos que pueden contener no a uno sólo, sino a una infinidad de sucesos elementales --y también no contener ninguno.-- Sucesos aleatorios que aparecen con gran frecuencia en el cálculo de probabilidades son los siguientes:
4.4.0.0.0.1 Suceso seguro: Es aquel que siempre se verifica después del experimento aleatorio, es decir, el mismo E
4.4.0.0.0.2 Suceso imposible: Es aquel que nunca se verifica como resultado del experimento aleatorio. Como debe ser un subconjunto de E, la única posibilidad es que el suceso imposible sea el conjunto vacío
4.4.0.0.0.3 Suceso contrario a un suceso A: También se denomina complementario de A y es el suceso que se verifica si, como resultado del experimento aleatorio, no se verifica A. Se acostumbra a denotar con el símbolo
Figura: Representación gráfica de un suceso aleatorio , y de su suceso contrario
4.4.0.1 Ejemplo Si realizamos el experimento aleatorio de lanzar un dado al aire, tenemos:
SUCESO ELEMENTALES:.......1,2,3,4,5,6
ESPACIO MUESTRAL:.........E= {,2,3,4,5,6}
SUCESOS ALEATORIOS........{0 ucesos imposibles.
E sucesos seguros
{1,2,3}
{4,5}
{2,4,6}= ---------
{1,2,3}
COMENTARIO SOBRE EXPERIMENTOS QUE NO SON ALEATORIOS...
CUANDO UNA MONEDA TIENE LA MISMA CARA...... NO ES UN OBJETO DEL ESTUDIO DE LA PROBABILIDAD
COMENTARIO......
La teoría de la probabilidad es la teoría matemática que modela los fenómenos aleatorios. cuando hablamos sobre lo que es aleatorio: es decir que puede representar diversos resultados dentro de un conjunto de posibles de soluciones en si la palabra aleatorio significa por ejemplo si lanzamos una moneda ahi tenemos dos posibles resultados, esta la cara, y el escudo. Estos son los fenómenos determinísticos, en los cuales el resultado de un experimento, realizado bajo condiciones determinadas, produce un resultado único o y previsto: por ejemplo, el agua calentada a 100 grados centígrados, a presión normal, se transforma en vapor. Un fenómeno aleatorio es aquel que, a pesar de realizarse el experimento bajo las mismas condiciones determinadas, tiene como resultados posibles un conjunto de alternativas, como el lanzamiento de un dado o de una moneda.
Los procesos reales que se modelizan como procesos aleatorios pueden no serlo realmente; cómo tirar una moneda o un dado no son procesos aleatorios en sentido estricto, ya que no se reproducen exactamente las mismas condiciones iniciales que lo determinan, sino sólo unas pocas. En los procesos reales que se modelizan mediante distribuciones de probabilidad corresponden a modelos complejos donde no se conocen a priori todos los parámetros que intervienen; ésta es una de las razones por las cuales la estadística, que busca determinar estos parámetros, no se reduce inmediatamente a la teoría de la probabilidad en sí.
Los procesos reales que se modelizan como procesos aleatorios pueden no serlo realmente; cómo tirar una moneda o un dado no son procesos aleatorios en sentido estricto, ya que no se reproducen exactamente las mismas condiciones iniciales que lo determinan, sino sólo unas pocas. En los procesos reales que se modelizan mediante distribuciones de probabilidad corresponden a modelos complejos donde no se conocen a priori todos los parámetros que intervienen; ésta es una de las razones por las cuales la estadística, que busca determinar estos parámetros, no se reduce inmediatamente a la teoría de la probabilidad en sí.
INTERPRETACION DE LA PROBABILIDAD Y SU HISTORIA
La palabra probabilidad no tiene una definición consistente. De hecho hay dos amplias categorías de interpretaciones de la probabilidad: los frecuentistas hablan de probabilidades sólo cuando se trata de experimentos aleatorios bien definidos. La frecuencia relativa de ocurrencia del resultado de un experimento, cuando se repite el experimento, es una medida de la probabilidad de ese suceso aleatorio. Los bayesianos, no obstante, asignan las probabilidades a cualquier declaración, incluso cuando no implica un proceso aleatorio, como una manera de representar su verosimilitud subjetiva.
Historia [editar]
Véase también: Estadística
El estudio científico de la probabilidad es un desarrollo moderno. Los juegos de azar muestran que ha habido un interés en cuantificar las ideas de la probabilidad durante milenios, pero las descripciones matemáticas exactas de utilidad en estos problemas sólo surgieron mucho después.
Según Richard Jeffrey, "Antes de la mitad del siglo XVII, el término 'probable' (en latín probable) significaba aprobable, y se aplicaba en ese sentido, unívocamente, a la opinión y a la acción. Una acción u opinión probable era una que las personas sensatas emprenderían o mantendrían, en las circunstancias."[1]
Aparte de algunas consideraciones elementales hechas por Girolamo Cardano en el siglo XVI, la doctrina de las probabilidades data de la correspondencia de Pierre de Fermat y Blaise Pascal (1654). Christiaan Huygens (1657) le dio el tratamiento científico conocido más temprano al concepto. Ars Conjectandi (póstumo, 1713) de Jakob Bernoulli y Doctrine of Chances (1718) de Abraham de Moivre trataron el tema como una rama de las matemáticas. Véase El surgimiento de la probabilidad (The Emergence of Probability) de Ian Hacking para una historia de los inicios del desarrollo del propio concepto de probabilidad matemática.
La teoría de errores puede trazarse atrás en el tiempo hasta Opera Miscellanea (póstumo, 1722) de Roger Cotes, pero una memoria preparada por Thomas Simpson en 1755 (impresa en 1756) aplicó por primera vez la teoría para la discusión de errores de observación. La reimpresión (1757) de esta memoria expone los axiomas de que los errores positivos y negativos son igualmente probables, y que hay ciertos límites asignables dentro de los cuales se supone que caen todos los errores; se discuten los errores continuos y se da una curva de la probabilidad.
Pierre-Simon Laplace (1774) hizo el primer intento para deducir una regla para la combinación de observaciones a partir de los principios de la teoría de las probabilidades. Representó la ley de la probabilidad de error con una curva y = φ(x), siendo x cualquier error e y su probabilidad, y expuso tres propiedades de esta curva:
es simétrica al eje y;
el eje x es una asíntota, siendo la probabilidad del error igual a 0;
la superficie cerrada es 1, haciendo cierta la existencia de un error.
Dedujo una fórmula para la media de tres observaciones. También obtuvo (1781) una fórmula para la ley de facilidad de error (un término debido a Lagrange, 1774), pero una que llevaba a ecuaciones inmanejables. Daniel Bernoulli (1778) introdujo el principio del máximo producto de las probabilidades de un sistema de errores concurrentes.
El método de mínimos cuadrados se debe a Adrien-Marie Legendre (1805), que lo introdujo en su Nouvelles méthodes pour la détermination des orbites des comètes (Nuevos métodos para la determinación de las órbitas de los cometas). Ignorando la contribución de Legendre, un escritor irlandés estadounidense, Robert Adrain, editor de "The Analyst" (1808), dedujo por primera vez la ley de facilidad de error,
siendo c y h constantes que dependen de la precisión de la observación. Expuso dos demostraciones, siendo la segunda esencialmente la misma de John Herschel (1850). Gauss expuso la primera demostración que parece que se conoció en Europa (la tercera después de la de Adrain) en 1809. Demostraciones adicionales se expusieron por Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W. F. Donkin (1844, 1856) y Morgan Crofton (1870). Otros personajes que contribuyeron fueron Ellis (1844), De Morgan (1864), Glaisher (1872) y Giovanni Schiaparelli (1875). La fórmula de Peters (1856) para r, el error probable de una única observación, es bien conocida.
En el siglo XIX, los autores de la teoría general incluían a Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, y Karl Pearson. Augustus De Morgan y George Boole mejoraron la exposición de la teoría.
En la parte geométrica (véase geometría integral) los colaboradores de The Educational Times fueron influyentes (Miller, Crofton, McColl, Wolstenholme, Watson y Artemas Martin).
Teoría [editar]
Artículo principal: Teoría de la probabilidad
La probabilidad constituye un importante parametro en la determinacion de las diversas causalidades obtenidas tras una serie de eventos esperados dentro de un rango estadistico.
Existen diversas formas como metodo abstracto, como la teoría Dempster-Shafer y la teoría de la relatividad numerica, esta ultima con un alto grado de aceptacion si se toma en cuenta que disminuye considerablemente las posibilidades hasta un nivel minimo ya que somete a todas las antiguas reglas a una simple ley de relatividad.
Aplicaciones [editar]
Dos aplicaciones principales de la teoría de la probabilidad en el día a día son en el análisis de riesgo y en el comercio de los mercados de materias primas. Los gobiernos normalmente aplican métodos probabilísticos en regulación ambiental donde se les llama "análisis de vías de dispersión", y a menudo miden el bienestar usando métodos que son estocásticos por naturaleza, y escogen qué proyectos emprender basándose en análisis estadísticos de su probable efecto en la población como un conjunto. No es correcto decir que la estadística está incluida en el propio modelado, ya que típicamente los análisis de riesgo son para una única vez y por lo tanto requieren más modelos de probabilidad fundamentales, por ej. "la probabilidad de otro 11-S". Una ley de números pequeños tiende a aplicarse a todas aquellas elecciones y percepciones del efecto de estas elecciones, lo que hace de las medidas probabilísticas un tema político.
Un buen ejemplo es el efecto de la probabilidad percibida de cualquier conflicto generalizado sobre los precios del petróleo en Oriente Medio - que producen un efecto dominó en la economía en conjunto. Un cálculo por un mercado de materias primas en que la guerra es más probable en contra de menos probable probablemente envía los precios hacia arriba o hacia abajo e indica a otros comerciantes esa opinión. Por consiguiente, las probabilidades no se calculan independientemente y tampoco son necesariamente muy racionales. La teoría de las finanzas conductuales surgió para describir el efecto de este pensamiento de grupo en el precio, en la política, y en la paz y en los conflictos.
Se puede decir razonablemente que el descubrimiento de métodos rigurosos para calcular y combinar los cálculos de probabilidad ha tenido un profundo efecto en la sociedad moderna. Por consiguiente, puede ser de alguna importancia para la mayoría de los ciudadanos entender cómo se cálculan los pronósticos y las probabilidades, y cómo contribuyen a la reputación y a las decisiones, especialmente en una democracia.
Otra aplicación significativa de la teoría de la probabilidad en el día a día es en la fiabilidad. Muchos bienes de consumo, como los automóviles y la electrónica de consumo, utilizan la teoría de la fiabilidad en el diseño del producto para reducir la probabilidad de avería. La probabilidad de avería también está estrechamente relacionada con la garantía del producto.
Se puede decir que no existe una cosa llamada probabilidad. También se puede decir que la probabilidad es la medida de nuestro grado de incertidumbre, o esto es, el grado de nuestra ignorancia dada una situación. Por consiguiente, puede haber una probabilidad de 1 entre 52 de que la primera carta en un baraja de cartas es la J de diamantes. Sin embargo, si uno mira la primera carta y la reemplaza, entonces la probabilidad es o bien 100% o 0%, y la elección correcta puede ser hecha con precisión por el que ve la carta. La física moderna proporciona ejemplos importantes de situaciones determinísticas donde sólo la descripción probabilística es factible debido a información incompleta y la complejidad de un sistema así como ejemplos de fenómenos realmente aleatorios.
En un universo determinista, basado en los conceptos newtonianos, no hay probabilidad si se conocen todas las condiciones. En el caso de una ruleta, si la fuerza de la mano y el periodo de esta fuerza es conocido, entonces el número donde la bola parará será seguro. Naturalmente, esto también supone el conocimiento de la inercia y la fricción de la ruleta, el peso, lisura y redondez de la bola, las variaciones en la velocidad de la mano durante el movimiento y así sucesivamente. Una descripción probabilística puede entonces ser más práctica que la mecánica newtoniana para analizar el modelo de las salidas de lanzamientos repetidos de la ruleta. Los físicos se encuentran con la misma situación en la teoría cinética de los gases, donde el sistema determinístico en principio, es tan complejo (con el número de moléculas típicamente del orden de magnitud de la constante de Avogadro ) que sólo la descripción estadística de sus propiedades es viable.
La mecánica cuántica, debido al principio de indeterminación de Heisenberg, sólo puede ser descrita actualmente a través de distribuciones de probabilidad, lo que le da una gran importancia a las descripciones probabilísticas. Algunos científicos hablan de la expulsión del paraíso.[cita requerida] Otros no se conforman con la pérdida del determinismo. Albert Einstein comentó estupendamente en una carta a Max Born: Jedenfalls bin ich überzeugt, daß der Alte nicht würfelt. (Estoy convencido de que Dios no tira el dado). No obstante hoy en día no existe un medio mejor para describir la física cuántica si no es a través de la teoría de la probabilidad. Mucha gente hoy en día confunde el hecho de que la mecánica cuántica se describe a través de distribuciones de probabilidad con la suposición de que es por ello un proceso aleatorio, cuando la mecánica cuántica es probabilística no por el hecho de que siga procesos aleatorios sino por el hecho de no poder determinar con precisión sus parámetros fundamentales, lo que imposibilita la creación de un sistema de ecuaciones determinista.
Historia [editar]
Véase también: Estadística
El estudio científico de la probabilidad es un desarrollo moderno. Los juegos de azar muestran que ha habido un interés en cuantificar las ideas de la probabilidad durante milenios, pero las descripciones matemáticas exactas de utilidad en estos problemas sólo surgieron mucho después.
Según Richard Jeffrey, "Antes de la mitad del siglo XVII, el término 'probable' (en latín probable) significaba aprobable, y se aplicaba en ese sentido, unívocamente, a la opinión y a la acción. Una acción u opinión probable era una que las personas sensatas emprenderían o mantendrían, en las circunstancias."[1]
Aparte de algunas consideraciones elementales hechas por Girolamo Cardano en el siglo XVI, la doctrina de las probabilidades data de la correspondencia de Pierre de Fermat y Blaise Pascal (1654). Christiaan Huygens (1657) le dio el tratamiento científico conocido más temprano al concepto. Ars Conjectandi (póstumo, 1713) de Jakob Bernoulli y Doctrine of Chances (1718) de Abraham de Moivre trataron el tema como una rama de las matemáticas. Véase El surgimiento de la probabilidad (The Emergence of Probability) de Ian Hacking para una historia de los inicios del desarrollo del propio concepto de probabilidad matemática.
La teoría de errores puede trazarse atrás en el tiempo hasta Opera Miscellanea (póstumo, 1722) de Roger Cotes, pero una memoria preparada por Thomas Simpson en 1755 (impresa en 1756) aplicó por primera vez la teoría para la discusión de errores de observación. La reimpresión (1757) de esta memoria expone los axiomas de que los errores positivos y negativos son igualmente probables, y que hay ciertos límites asignables dentro de los cuales se supone que caen todos los errores; se discuten los errores continuos y se da una curva de la probabilidad.
Pierre-Simon Laplace (1774) hizo el primer intento para deducir una regla para la combinación de observaciones a partir de los principios de la teoría de las probabilidades. Representó la ley de la probabilidad de error con una curva y = φ(x), siendo x cualquier error e y su probabilidad, y expuso tres propiedades de esta curva:
es simétrica al eje y;
el eje x es una asíntota, siendo la probabilidad del error igual a 0;
la superficie cerrada es 1, haciendo cierta la existencia de un error.
Dedujo una fórmula para la media de tres observaciones. También obtuvo (1781) una fórmula para la ley de facilidad de error (un término debido a Lagrange, 1774), pero una que llevaba a ecuaciones inmanejables. Daniel Bernoulli (1778) introdujo el principio del máximo producto de las probabilidades de un sistema de errores concurrentes.
El método de mínimos cuadrados se debe a Adrien-Marie Legendre (1805), que lo introdujo en su Nouvelles méthodes pour la détermination des orbites des comètes (Nuevos métodos para la determinación de las órbitas de los cometas). Ignorando la contribución de Legendre, un escritor irlandés estadounidense, Robert Adrain, editor de "The Analyst" (1808), dedujo por primera vez la ley de facilidad de error,
siendo c y h constantes que dependen de la precisión de la observación. Expuso dos demostraciones, siendo la segunda esencialmente la misma de John Herschel (1850). Gauss expuso la primera demostración que parece que se conoció en Europa (la tercera después de la de Adrain) en 1809. Demostraciones adicionales se expusieron por Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W. F. Donkin (1844, 1856) y Morgan Crofton (1870). Otros personajes que contribuyeron fueron Ellis (1844), De Morgan (1864), Glaisher (1872) y Giovanni Schiaparelli (1875). La fórmula de Peters (1856) para r, el error probable de una única observación, es bien conocida.
En el siglo XIX, los autores de la teoría general incluían a Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, y Karl Pearson. Augustus De Morgan y George Boole mejoraron la exposición de la teoría.
En la parte geométrica (véase geometría integral) los colaboradores de The Educational Times fueron influyentes (Miller, Crofton, McColl, Wolstenholme, Watson y Artemas Martin).
Teoría [editar]
Artículo principal: Teoría de la probabilidad
La probabilidad constituye un importante parametro en la determinacion de las diversas causalidades obtenidas tras una serie de eventos esperados dentro de un rango estadistico.
Existen diversas formas como metodo abstracto, como la teoría Dempster-Shafer y la teoría de la relatividad numerica, esta ultima con un alto grado de aceptacion si se toma en cuenta que disminuye considerablemente las posibilidades hasta un nivel minimo ya que somete a todas las antiguas reglas a una simple ley de relatividad.
Aplicaciones [editar]
Dos aplicaciones principales de la teoría de la probabilidad en el día a día son en el análisis de riesgo y en el comercio de los mercados de materias primas. Los gobiernos normalmente aplican métodos probabilísticos en regulación ambiental donde se les llama "análisis de vías de dispersión", y a menudo miden el bienestar usando métodos que son estocásticos por naturaleza, y escogen qué proyectos emprender basándose en análisis estadísticos de su probable efecto en la población como un conjunto. No es correcto decir que la estadística está incluida en el propio modelado, ya que típicamente los análisis de riesgo son para una única vez y por lo tanto requieren más modelos de probabilidad fundamentales, por ej. "la probabilidad de otro 11-S". Una ley de números pequeños tiende a aplicarse a todas aquellas elecciones y percepciones del efecto de estas elecciones, lo que hace de las medidas probabilísticas un tema político.
Un buen ejemplo es el efecto de la probabilidad percibida de cualquier conflicto generalizado sobre los precios del petróleo en Oriente Medio - que producen un efecto dominó en la economía en conjunto. Un cálculo por un mercado de materias primas en que la guerra es más probable en contra de menos probable probablemente envía los precios hacia arriba o hacia abajo e indica a otros comerciantes esa opinión. Por consiguiente, las probabilidades no se calculan independientemente y tampoco son necesariamente muy racionales. La teoría de las finanzas conductuales surgió para describir el efecto de este pensamiento de grupo en el precio, en la política, y en la paz y en los conflictos.
Se puede decir razonablemente que el descubrimiento de métodos rigurosos para calcular y combinar los cálculos de probabilidad ha tenido un profundo efecto en la sociedad moderna. Por consiguiente, puede ser de alguna importancia para la mayoría de los ciudadanos entender cómo se cálculan los pronósticos y las probabilidades, y cómo contribuyen a la reputación y a las decisiones, especialmente en una democracia.
Otra aplicación significativa de la teoría de la probabilidad en el día a día es en la fiabilidad. Muchos bienes de consumo, como los automóviles y la electrónica de consumo, utilizan la teoría de la fiabilidad en el diseño del producto para reducir la probabilidad de avería. La probabilidad de avería también está estrechamente relacionada con la garantía del producto.
Se puede decir que no existe una cosa llamada probabilidad. También se puede decir que la probabilidad es la medida de nuestro grado de incertidumbre, o esto es, el grado de nuestra ignorancia dada una situación. Por consiguiente, puede haber una probabilidad de 1 entre 52 de que la primera carta en un baraja de cartas es la J de diamantes. Sin embargo, si uno mira la primera carta y la reemplaza, entonces la probabilidad es o bien 100% o 0%, y la elección correcta puede ser hecha con precisión por el que ve la carta. La física moderna proporciona ejemplos importantes de situaciones determinísticas donde sólo la descripción probabilística es factible debido a información incompleta y la complejidad de un sistema así como ejemplos de fenómenos realmente aleatorios.
En un universo determinista, basado en los conceptos newtonianos, no hay probabilidad si se conocen todas las condiciones. En el caso de una ruleta, si la fuerza de la mano y el periodo de esta fuerza es conocido, entonces el número donde la bola parará será seguro. Naturalmente, esto también supone el conocimiento de la inercia y la fricción de la ruleta, el peso, lisura y redondez de la bola, las variaciones en la velocidad de la mano durante el movimiento y así sucesivamente. Una descripción probabilística puede entonces ser más práctica que la mecánica newtoniana para analizar el modelo de las salidas de lanzamientos repetidos de la ruleta. Los físicos se encuentran con la misma situación en la teoría cinética de los gases, donde el sistema determinístico en principio, es tan complejo (con el número de moléculas típicamente del orden de magnitud de la constante de Avogadro ) que sólo la descripción estadística de sus propiedades es viable.
La mecánica cuántica, debido al principio de indeterminación de Heisenberg, sólo puede ser descrita actualmente a través de distribuciones de probabilidad, lo que le da una gran importancia a las descripciones probabilísticas. Algunos científicos hablan de la expulsión del paraíso.[cita requerida] Otros no se conforman con la pérdida del determinismo. Albert Einstein comentó estupendamente en una carta a Max Born: Jedenfalls bin ich überzeugt, daß der Alte nicht würfelt. (Estoy convencido de que Dios no tira el dado). No obstante hoy en día no existe un medio mejor para describir la física cuántica si no es a través de la teoría de la probabilidad. Mucha gente hoy en día confunde el hecho de que la mecánica cuántica se describe a través de distribuciones de probabilidad con la suposición de que es por ello un proceso aleatorio, cuando la mecánica cuántica es probabilística no por el hecho de que siga procesos aleatorios sino por el hecho de no poder determinar con precisión sus parámetros fundamentales, lo que imposibilita la creación de un sistema de ecuaciones determinista.
LA PROBABILIDAD
La probabilidad mide la frecuencia con la que ocurre un resultado en un experimento bajo condiciones suficientemente estables. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la matemática, la ciencia y la filosofía para sacar conclusiones sobre la probabilidad La palabra probabilidad no tiene una definición consistente. De hecho hay dos amplias categorías de interpretaciones de la probabilidad: los frecuentistas hablan de probabilidades sólo cuando se trata de experimentos aleatorios bien definidos. La frecuencia relativa de ocurrencia del resultado de un experimento, cuando se repite el experimento, es una medida de la probabilidad de ese suceso aleatorio. Los bayesianos, no obstante, asignan las probabilidades a cualquier declaración, incluso cuando no implica un proceso aleatorio, como una manera de representar su verosimilitud subjetiva.de sucesos potenciales y la mecánica subyacente de sistemas complejos.
lunes, 28 de julio de 2008
CLASES DE TENDENCIA
CONSTANTE:
Está utiliza el algoritmo de marquardt en arima, que puede ser mas exacto.es un valor grande y para esta constante suele ser indicativo de problelmas condicionamiento en todos los datos . Generalmente esta constante debe ser casi igual a cero cuando se obtienen muchas estimaciones finales.
COMENTARIO:
Una tendencia costante tiene que ser igual a cero ya que por medio de ella obtenemos la estimacion con una exactitud
Está utiliza el algoritmo de marquardt en arima, que puede ser mas exacto.es un valor grande y para esta constante suele ser indicativo de problelmas condicionamiento en todos los datos . Generalmente esta constante debe ser casi igual a cero cuando se obtienen muchas estimaciones finales.
COMENTARIO:
Una tendencia costante tiene que ser igual a cero ya que por medio de ella obtenemos la estimacion con una exactitud
CLASIFICACION DE SERIES TEMPORALES
SERIE ESTACIONARIA
Implica que no importa cual segmento de las serie se observe, no importa la longitud, la medida y la varianza deben ser similares.
Es constante a lo largo del tiempo para muchas aplicaciones practicas se considera la llamada estacionariedad.
Cuando se encuentra en equilibrio estadistico, en el sentido de que sus propiedades no varian a lo largo del tiempo, y por lo tanto no pueden existir tendencias.
COMENTARIO:
UNA SERIE DE TIEMPO ESTACIONARIA, ES AQUELLA QUE EXPLICA LOS PASOS DE LOS DATOS O VALORES QUE NO REPRESENTAN NINGUN CAMBIO A LO LARGO DEL TIEMPO COMO EN LA MEDIA Y EN LA VARIANZA.
Implica que no importa cual segmento de las serie se observe, no importa la longitud, la medida y la varianza deben ser similares.
Es constante a lo largo del tiempo para muchas aplicaciones practicas se considera la llamada estacionariedad.
Cuando se encuentra en equilibrio estadistico, en el sentido de que sus propiedades no varian a lo largo del tiempo, y por lo tanto no pueden existir tendencias.
COMENTARIO:
UNA SERIE DE TIEMPO ESTACIONARIA, ES AQUELLA QUE EXPLICA LOS PASOS DE LOS DATOS O VALORES QUE NO REPRESENTAN NINGUN CAMBIO A LO LARGO DEL TIEMPO COMO EN LA MEDIA Y EN LA VARIANZA.
CLASIFICACION DE SERIES TEMPORALES
Una serie de tiempo no estacionaria no tiene medida a largo plazo a la cual la serie vuelva su varianza aumenta, con el tiempo tendiendo al infinito.
Una serie de tiempo no estacionaria puede tener tendencias deterministas, estocasticas o ambas simultaneamente.
Una serie de tiempo no estacionaria si sus propiedades varian con el tiempo
COMENTARIO:
UNA SERIE DE TIEMPO NO ESTACIONARIA, ES AQUELLA
QUE REPRESENTA CAMBIOS, Y NO TIENE MEDIDA A LO
LARGO DEL TIEMPO Y ES INFINITO.
Una serie de tiempo no estacionaria puede tener tendencias deterministas, estocasticas o ambas simultaneamente.
Una serie de tiempo no estacionaria si sus propiedades varian con el tiempo
COMENTARIO:
UNA SERIE DE TIEMPO NO ESTACIONARIA, ES AQUELLA
QUE REPRESENTA CAMBIOS, Y NO TIENE MEDIDA A LO
LARGO DEL TIEMPO Y ES INFINITO.
Series de Tiempo
Una serie temporal o cronologica es un conjunto e observaciones de una variable, ordenadas segu transcurre el tiempo.
En una serie de tiempo las observaciones no se deben ordenar de mayor a menor debidoa que se perderia el grueso de la informacion debido a que nos intersea detectar como se mueve la variable en el tiempo es muy importante respetar la secuencia temporal de las observaciones.
Representacion de una Serie Temporal
Par realizar la reprsenyacion de una serie ytemporal se debe realizae mediante una gráfica de disprsión x-y
En una serie de tiempo las observaciones no se deben ordenar de mayor a menor debidoa que se perderia el grueso de la informacion debido a que nos intersea detectar como se mueve la variable en el tiempo es muy importante respetar la secuencia temporal de las observaciones.
Representacion de una Serie Temporal
Par realizar la reprsenyacion de una serie ytemporal se debe realizae mediante una gráfica de disprsión x-y
 COMENTARIO:
COMENTARIO:
SON CONJUNTOS DE DATOS QUE SE LOGRAN DETERMINAR CON EL TIEMPO DE MANERA MAS FACIL Y RAPIDA PARA REALIZAR UN BUEN NUMERO DE FENOMENOS REALES Y POR MEDIO DE SU EJE VERTICAL LOGRAMOS INDICAR LOS VALORES QUE SE OBSERVARON
sábado, 7 de junio de 2008
COMENTARIO:
LA CORRELACIÓN: Son datos que pueden cambiar de valores, a lo largo de la ejecución, que es el valor que corresponde a un tipo de datos y como también es sustituido por un valor cualquiera, y nos ayuda a analizar la relación entre diferentes variables, y como también se asocia a cada elemento de su fórmula, además nos sirve determinar el grado de relación, por ejemplo: el grado de conocimiento sobre el SIDA, en adolentes.y como también tiene dos pendiente una positiva, cuando va a la derecha y una negativa cuando va a la izquierda, y como también puede ser débil cuando está cercano a (0), y puede ser positiva fuerte, y por medio de su forma que es punto pendiente, ecuación general de una línea recta, forma estándar, forma general,podemos operar las variable que nos lo plantea el catedrático. y se opera sustituyendo dichos valores y se puede operar por medio de línea de pearson, pero ajustando bien la línea. y por último estas dos operaciones tanto como sustituidos y graficado tiene que dar un resultado iguales pero de lo contrario estará mal la operación realizada, además antes de operar una tarea tiene que coincidir las dos variables con relación a la otra. por el contrario no va haber relación entre las dos variables.
FUERZA, SENTIDO Y LA FORMA DE CORRELÓN:
La relación entre dos variables cuantitativas queda representada mediante la línea de mejor ajuste, trazada a partir de la nube de puntos. Los principales componentes elementales de una línea de ajuste y, por lo tanto, de unan correlación , son la fuerza, y el sentido y la forma:
LA FUERZA: Mide el grado en que la línea representa a la nube de puntos: si la nube es estrecha y alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos tiene una tendencia elíptica o circular, la relación es débil.
EL SENTIDO: Mide la variación de los valores de B con respecto a A: si al crecer los valores de A lo hacen los de B, la relación es positiva; si al crecer los valores de A disminuyen los de B, la relación es negativa.
LA FORMA: Establece el tipo de línea que define el mejor ajuste,la línea recta, la curva monotónica, o la curva no monotónica.
LA FUERZA: Mide el grado en que la línea representa a la nube de puntos: si la nube es estrecha y alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos tiene una tendencia elíptica o circular, la relación es débil.
EL SENTIDO: Mide la variación de los valores de B con respecto a A: si al crecer los valores de A lo hacen los de B, la relación es positiva; si al crecer los valores de A disminuyen los de B, la relación es negativa.
LA FORMA: Establece el tipo de línea que define el mejor ajuste,la línea recta, la curva monotónica, o la curva no monotónica.
CORRELACIÓN:
En probabilidad y estadística, la correlacion indica la fuerza y la dirección de una relación lineal entre dos variables aleatorias. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas se varían sistemáticamente con respecto a los valores homónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo haces también los de B y viceversa. La correlación entre dos variables no implica, por si misma , ninguna relación de causalidad...
sábado, 24 de mayo de 2008
CARACTERÍSTICA:
EL DIAGRAMA DE CAJAS O BIGOTES PUEDE PRESENTARSE SIMÉTRICAS, ASIMÉTRICAS, POSITIVA O NEGATIVA SEGUN LA LÍNEA QUE REPRESENTA...........
viernes, 23 de mayo de 2008
domingo, 18 de mayo de 2008
RELACION ENTRE LA CURVA NORMAL Y DIAGRAMA DE CAJAS (COMENTARIO)
AMBOS DESCRIBEN LAS CARACTERÍSTICAS DE UN CONJUNTO DE DATOS Y CADA UNA DE ELLAS TIENEN SUS CIERTAS FÓRMULAS AL PODER OPERARLOS, Y COMO TAMBIÉN NOS AYUDA A CONOCER LA MEDIDA DEL CENTRO DE DICHAS GRÁFICAS TANTO COMO LA CURVA Y EL DIAGRAMA DE CAJA ,ENCONTRAMOS EL ALEJAMIENTO DE LA SIMETRÍA. Y EN LAS DOS SE UBICA LA MEDIA, SOLO QUE EN LA CURVA NO SE UBICAN LOS CUARTILES PERO CASI SE MANEJA IGUAL. SOLO QUE LA DIAGRAMA SE LE PONE UN PUNTO DONDE QUEDA LA MEDIA PERO SI EN LAS DOS SE USA LA LÍNEA RECTA .
COMENTARIO:
EL DIAGRAMA DE CAJAS ES UNA REPRESENTACION GRAFICA DE FORMA RECTANGULAR QUE ANTES DE EMPEZAR A GRAFICAR TENEMOS QUE TENER LOS CUARTILES Y ENCONTRAR QUE TNA ALEJADOS ESTAN LOS DATOS A LA MEDIANA, Y COMO TAMBIEN ES UNA FORMA MAS FACIL Y PRÁCTICO DE UTILIZAR Y ATRAVÉZ DE ESTO NOS DA A CONOCER UNA MEDIDA DE LA SIMETRÍA O ASIMETRÍA DE DIFERENTES DISTRIBUCIONES Y ESTO NOS AYUDA A DESCRIBIR LAS CARÁCTERISTICAS DE UN CONJUNDO DE DATOS BRUTOS (NO ORDENADOS) Y COMO TAMBIEN ATRAVEZ DE ESTO USAMOS LO QUE ES EL PASO DE TALLOS Y HOJAS COMO UN PROCEDIMIENTO Y LUEGO LO PREORDENAMOS, DESPUES SE CREA UNA TABLA AGRUPADA, DESPUES SE SACAN SU MEDIA Y DESPUES LOS CUARTILES, DESPUES SE SACA EL RANGO INTERCUARTÍLICO, MULTIPLICANDO POR EL 1.5 PARA OBTENER LA POSICIÓN DE LA BARRERA INTERIOR, Y DESPUÉS PARA OBTENER LA POSICIÓN DE LA BARRERA EXTERIOR, SE MULTIPLICA POR 3. Y POR ÚLTIMO SE GRÁFICA PRIMERO UBICAMOS EL PRIMER CUARTIL, Y DESPUES LA MEDIA SE LE MARCA UNA X EN LA GRÁFICA RECTANGULAR, Y DESPUES SE UBICA EL CUARTIL DOS, Y DE ÚLTIMO EL CUARTIL TRES Y EN CADA POSICION DEL LADO DERECHO E IZQUIERDO SE CREA EL BIGOTE DEPENDE DE LA CANTIDA QUE SE SACA DE DICHOS POSICIONES. A UNO RESTANDO Y AL OTRO SUMANDO ...
DIAGRAMA DE CAJAS (BOX PLOT)
ES UN GRAFICO; BASADO EN CUARTILES; MEDIANTE EL CUAL SE VISUALIZA UN CONJUNTO DE DAROS: LA INFORMACION QUE BUSCA ES SOBRE LA MEDIANA Y EL Q1 Y Q3 SOBRE LA EXISTENCIA DE DATOS ATIPICOS DE LA DISTRIBUCION...
COMENTARIO
VALOR DE Z ES COMO UN VALOR RESUMIDO Y CALCULADO, EN LA CUAL SE PODRÁ DAR CUENTA QUE LA MEDIA Y LA DESVIACIÓN ESTÁNDAR, DEBEMOS DE TENER SUS VALORES PARA PODER OBTENER SUS PORCENTAJES Y LUEGO OBTENEMOS EL VALOR DE "Z". Y SI EN DADO CASO LA "X", ES MAYOR QUE LA MEDIA ENTONCES LA "Z", SERÁ POSITIVA, Y SI ES MENOR SERÁ NEGATIVA, Y CUANDO ES IGUAL, EL VALOR SERÁ NULO, Y LA FORMÚLA QUE SE PUEDE UTILIZAR PARA UBICAR LA VARIANZAES: Z= X-DIVIDIDA LA DESVIACIÖN ESTANDAR Y RESPECTO A LA MEDIA:
COMENTARIO
SE PUEDE INTERPRETAR POR MEDIO DE UNA CURVA EN LA CUAL TIENE EL 100% Y SE DIVIDE POR MEDIO DE LA MEDIA , YA QUE ES EL DATO QUE SE ENCUENTRA BIEN CONCENTRADO A LA MITAD DE LA CURVA, Y COMO TAMBIÉN POR MEDIO DE LA FÓRMULA QUE TIENE QUE ES "Z", PODEMOS DETERMINAR EL PORCENTAJE QUE SE UBIQUE DENTRO DE CIERTOS LÍMITES MENCIONADOS.
DISTRIBUCION DE PORCENTAJES BAJO LA CURVA (GRÁFICA)
Ejemplos:
1. El acero que se utiliza para tuberías de agua a menudo se recubre internamente con un mortero de cemento para evitar la corrosión. En un estudio de los recubrimientos de mortero de una tubería empleada en un proyecto de transmisión de agua en California (Transportation Engineering Journal, Noviembre de 1979) se especificó un espesor de 7/16 pulgadas para el mortero. Un gran número de mediciones de espesor dieron una media de 0.635 pulgadas y una desviación estándar de 0.082 pulgadas. Sí las mediciones de espesor, tenían una distribución Normal, ¿qué porcentaje aproximado fue inferior a 7/16 de pulgada?
Solución:
x = variable que nos define el espesor del mortero en pulgadas
m = 0.635 pulgadas
s = 0.082 pulgadas
X = 7/16
m=0.635
Z
Ejemplos:
1. El acero que se utiliza para tuberías de agua a menudo se recubre internamente con un mortero de cemento para evitar la corrosión. En un estudio de los recubrimientos de mortero de una tubería empleada en un proyecto de transmisión de agua en California (Transportation Engineering Journal, Noviembre de 1979) se especificó un espesor de 7/16 pulgadas para el mortero. Un gran número de mediciones de espesor dieron una media de 0.635 pulgadas y una desviación estándar de 0.082 pulgadas. Sí las mediciones de espesor, tenían una distribución Normal, ¿qué porcentaje aproximado fue inferior a 7/16 de pulgada?
Solución:
x = variable que nos define el espesor del mortero en pulgadas
m = 0.635 pulgadas
s = 0.082 pulgadas
X = 7/16
m=0.635
Z
p(z = -2.41) = 0.492
p(x < 7/16 pulgadas) = 0.5- p(z = -2.41) = 0.5-0.492 = 0.008
Por tanto, 0.008 x 100% = 0.8% de los recubrimientos de mortero tienen un espesor menor de 7/16 pulgadas
1. El acero que se utiliza para tuberías de agua a menudo se recubre internamente con un mortero de cemento para evitar la corrosión. En un estudio de los recubrimientos de mortero de una tubería empleada en un proyecto de transmisión de agua en California (Transportation Engineering Journal, Noviembre de 1979) se especificó un espesor de 7/16 pulgadas para el mortero. Un gran número de mediciones de espesor dieron una media de 0.635 pulgadas y una desviación estándar de 0.082 pulgadas. Sí las mediciones de espesor, tenían una distribución Normal, ¿qué porcentaje aproximado fue inferior a 7/16 de pulgada?
Solución:
x = variable que nos define el espesor del mortero en pulgadas
m = 0.635 pulgadas
s = 0.082 pulgadas
X = 7/16
m=0.635
Z
Ejemplos:
1. El acero que se utiliza para tuberías de agua a menudo se recubre internamente con un mortero de cemento para evitar la corrosión. En un estudio de los recubrimientos de mortero de una tubería empleada en un proyecto de transmisión de agua en California (Transportation Engineering Journal, Noviembre de 1979) se especificó un espesor de 7/16 pulgadas para el mortero. Un gran número de mediciones de espesor dieron una media de 0.635 pulgadas y una desviación estándar de 0.082 pulgadas. Sí las mediciones de espesor, tenían una distribución Normal, ¿qué porcentaje aproximado fue inferior a 7/16 de pulgada?
Solución:
x = variable que nos define el espesor del mortero en pulgadas
m = 0.635 pulgadas
s = 0.082 pulgadas
X = 7/16
m=0.635
Z
p(z = -2.41) = 0.492
p(x < 7/16 pulgadas) = 0.5- p(z = -2.41) = 0.5-0.492 = 0.008
Por tanto, 0.008 x 100% = 0.8% de los recubrimientos de mortero tienen un espesor menor de 7/16 pulgadas
COMENTARIO:
ESTE PORTAFOLIO ES UNA TACTICA EN LA ENSEÑANZA DE LA EDUCACIÓN, EL EL MISMO SE PRESENTAN TEMAS DE GRAN IMPORTANCIA, PARA LA VIDAD DIARIA COMO LO ES ÁREA BAJO LA CURVA, ENTRE OTROS.........
EL PORTA FOLIO
ES UN DOCUMENTO DÓNDE LOS ESTUDIANTES LES SIRVEN COMO CARTERA DE TRABAJO Y DE CARÁCTER ESTADISTICO........
COMENTARIO:
LA CURVA ES UNA HERRAMIENTA EN QUE NOS HACE MÁS FÁCIL DE CALCULAR LA PROBABILIDAD DE UN SUCESO, COMO TAMBIÉN SE PUEDE DECIR QUE ES IGUAL A: 1, QUE EQUIVALE EL 100% DE LO CASOS . Y ADEMÁS EL EJE Y LO DIVIDE LA CURVA EN DOS PARTES IGUALES ES DECIR QUE EL 50% ESTÁN A CADA LADO. Y COMO TAMBIÉN LA MEDIA ES EL DATO QUE SE ENCUENTRA BIEN CONCENTRADO EN LA CURVA. Y POR ÚLTIMO NOS AYUDA A UBICARNOS A ENCONTRAR EL PORCENTAJE DE UN PROBLEMA DE ESTADÍSTICA..........
ÁREA BAJO LA CURVA
LA CURVA NORMAL TIENE FORMA DE CAMPANA LA MEDIA, LA MODA Y MEDIA DE LA DISTRIBUCIÓN SON IGUALES ...........
AREA BAJO LA CURVA
CONSISTE EN CALCULAR EL ÁREA DE LA LIMITADA ENTRE DOS PUNTOS DEL QUE REPRESENTA A UNA FUNCIÓN TEMÁTICA.
miércoles, 14 de mayo de 2008
COMENTARIO
ES UNA GRAFICA DE CARACTER ESTADISTICO, EN DONDE PODEMOS UBICAR LA MEDIA, MEDIANA, MODA, Y A LA VEZ OBSERVAR LA DISPERSION QUE EXISTE ENTRE CADA DATOS MENCIONADOS ANTERIORMENTE..........
AREA BAJO LA CURVA NORMAL
La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss". La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas generalmente por y . Con esta notación, la densidad de la normal viene dada por la ecuación:
COMENTARIO
ES UN TRABAJO QUE DEBE REALIZAR A DIARIO EL ALUMNO,(A). DE LO QUE APRENDE EN CLASE. Y COMO TAMBIEN NOS AYUDA A LLEVAR UN CONTROL DE EJERCICIOS ELABORADOS YA SEAN EN EQUIPO E INDIVIDUAL.........
que es portafolio
EL PORTAFOLIO DEL ESTUDIANTE
Definición: El Portafolio es un método de enseñanza, aprendizaje y evaluación que consiste en la aportación de
producciones de diferente índole por parte del estudiante a través de las cuáles se pueden juzgar sus
capacidades en el marco de una disciplina o materia de estudio. Estas producciones informan del
proceso personal seguido por el estudiante, permitiéndole a él y los demás ver sus esfuerzos y logros,
en relación a los objetivos de aprendizaje y criterios de evaluación establecidos previamente.
El portafolio como modelo de enseñanza - aprendizaje, se fundamenta en la teoría de que la
evaluación marca la forma cómo un estudiante se plantea su aprendizaje.
El portafolio del estudiante responde a dos aspectos esenciales del proceso de enseñanza-aprendizaje,
implica toda una metodología de trabajo y de estrategias didácticas en la interacción entre docente y
discente; y, por otro lado, es un método de evaluación que permite unir y coordinar un conjunto de
evidencias para emitir una valoración lo más ajustada a la realidad que es difícil de adquirir con otros
instrumentos de evaluación más tradicionales que aportan una visión más fragmentada.
Definición: El Portafolio es un método de enseñanza, aprendizaje y evaluación que consiste en la aportación de
producciones de diferente índole por parte del estudiante a través de las cuáles se pueden juzgar sus
capacidades en el marco de una disciplina o materia de estudio. Estas producciones informan del
proceso personal seguido por el estudiante, permitiéndole a él y los demás ver sus esfuerzos y logros,
en relación a los objetivos de aprendizaje y criterios de evaluación establecidos previamente.
El portafolio como modelo de enseñanza - aprendizaje, se fundamenta en la teoría de que la
evaluación marca la forma cómo un estudiante se plantea su aprendizaje.
El portafolio del estudiante responde a dos aspectos esenciales del proceso de enseñanza-aprendizaje,
implica toda una metodología de trabajo y de estrategias didácticas en la interacción entre docente y
discente; y, por otro lado, es un método de evaluación que permite unir y coordinar un conjunto de
evidencias para emitir una valoración lo más ajustada a la realidad que es difícil de adquirir con otros
instrumentos de evaluación más tradicionales que aportan una visión más fragmentada.
lunes, 7 de abril de 2008
jueves, 27 de marzo de 2008
MEDIA GEOMETRICA
De una serie de numeros es la raiz n-esima del producto de esos numeros se utiliza en el calculo de tasas de crecimiento.
MEDIA CUADRATICA
De uuna serie de numeros es la raiz cuadrada de la media aritmetica del cuadrado dedichos numeros.
MEDIA ARMONICA
Es el numero inverso de la media aritmetica de los inversos de cada uno de los datos de la serie.
MEDIA ARITMETICA
La media aritmetica de una serie estadistica es un valor tal que si con el constituye los terminos de una serie se puede obtener una suma igual a la que los propios terminos darian. la media aritmetica de sierto numero de cantidades es la suma de sus valores dividido por el numero total de ellas.
ESCALA DE LIKERT
La escala de Likert es una escala ordinal y como tal no mide en cuánto es más favorable o desfavorable una actitud, es decir que si una persona obtiene una puntuación de 60 puntos en una escala, no significa esto que su actitud hacia el fenómeno medido sea doble que la de otro individuo que obtenga 30 puntos, pero sí nos informa que el que obtiene 60 puntos tiene una actitud más favorable que el que tiene 30, de la misma forma que 40°C no son el doble de 20°C pero sí indican una temperatura más alta.
DIAGRAMA DE CAJAS
Es una ilustracion grafica basada en cuartiles, que ayuda a visualizar un conjunto de datos se requiere cinco tipos de datos para construir un diagrama de cajas: el valor minimo, el primer cuartil, la mediana, el tercer cuartil, y el valor maximo.
DIAGRAMA DE TALLOS Y HOJAS
Un diagrama donde cada valor de datos es dividido en una "hoja" (normalmente el último dígito) y un "tallo" (los otros dígitos). Por ejemplo "32" sería dividido en "3" (tallo) y "2" (hoja).Los valores del "tallo" se escriben hacia abajo y los valores "hoja" van a la derecha (o izquierda) del los valores tallo.El "tallo" es usado para agrupar los puntajes y cada "hoja" indica los puntajes individuales dentro de cada grupo.
ESCALA ORDINAL
Esta solo permite la identificacion y diferenciacion de los sujetos sino que a demas permite establecer relaciones del tipo (mayor que) o (menor que) es decir que de los sujetos se pueden decir cuales presentan mayor o menor magnitud de la caracteristica medida y los objetos se pueden ordenar por ejemplo nivel de estudios, posicion relativa en la clase,etc.
ESCALA NOMINAL
se utiliza como medidas de edentidad, es decir que nos permite identificar sujetos como iguales o diferentes los numeros sirven de indicativos para identificar objetos o clases por ejemplo las personas se pueden clasificar segun el sexo, su religion, el color de ojos etc.
VARIABLE
Es la caracteristica de los elementos de una poblacion que puede tener diferentes valores en los distintos elementos o individuos de un conjunto.
miércoles, 26 de marzo de 2008
chebychev
Esto nos sirve para ver en que lado estan`posicionados los datos porque si los datos estan empiricos la curva si tiene forma de campana.
Suscribirse a:
Entradas (Atom)


